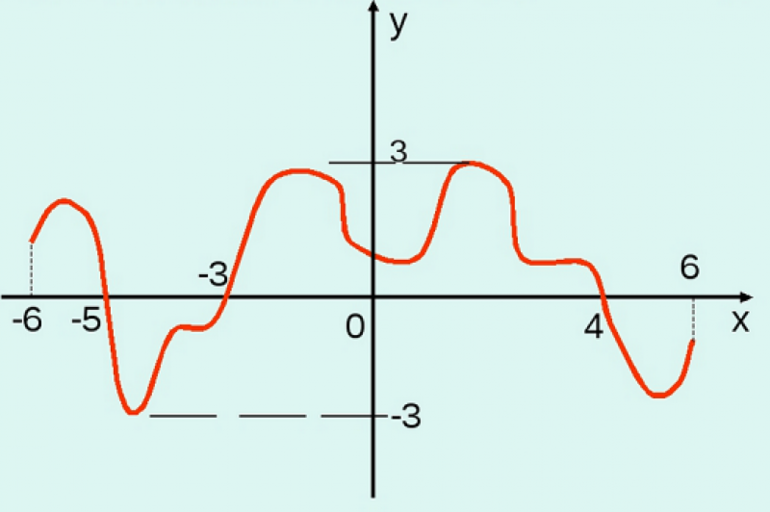
Озф в алгебре что это

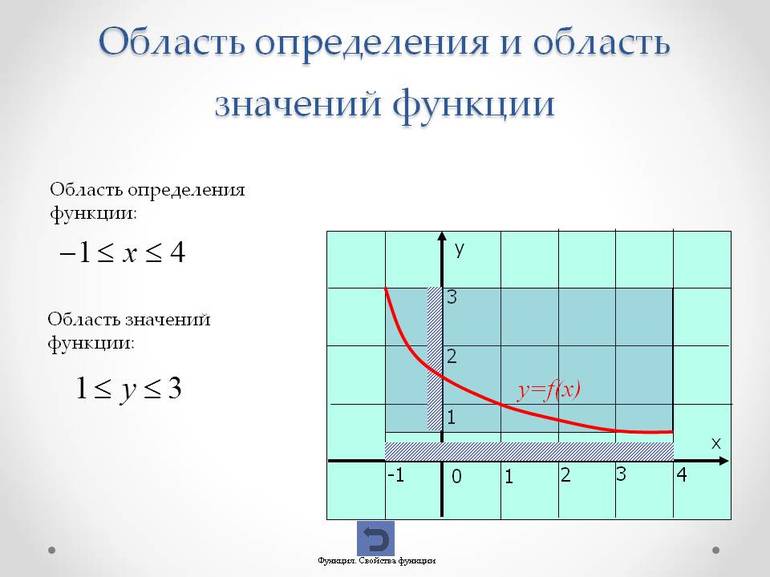
Область определения и область значений функции

Областью определения числовой функции (ООФ) называется множество числовых значений, которые может принимать аргумент x, так чтобы функция имела смысл.

ООФ – это основная характеристика любой функции, с учетом которой исследуются все остальные характеристики;

ООФ находится чаще всего как подмножество X множества действительных чисел , на котором выполнимы все операции, определяющие значение функции y по значению ее аргумента x; в этом случае ООФ называют естественной областью определения функциии она совпадает с областью допустимых значений (ОДЗ) для пенременной в выражении f(x);

ООФ может находиться по смыслу функции и в этом случае она будет более узкой, чем естественная ООФ;

приняты и другие обозначения ООФ, например, D(f) или D(y).

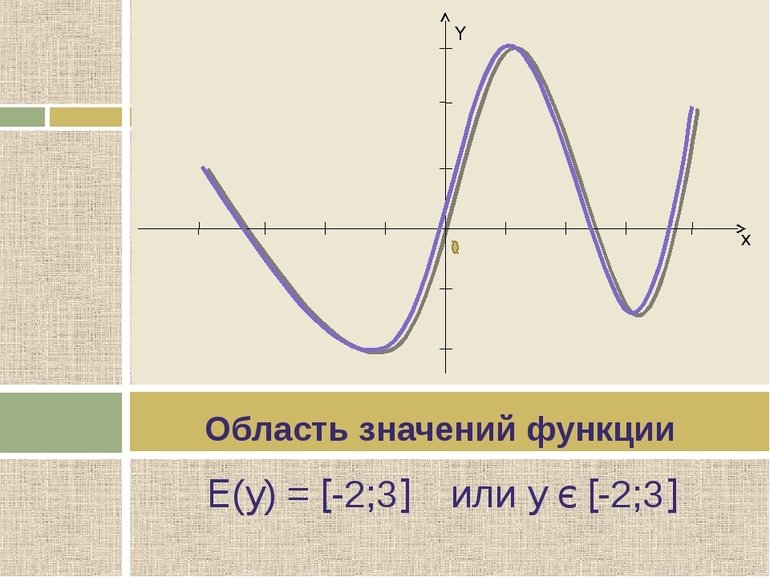
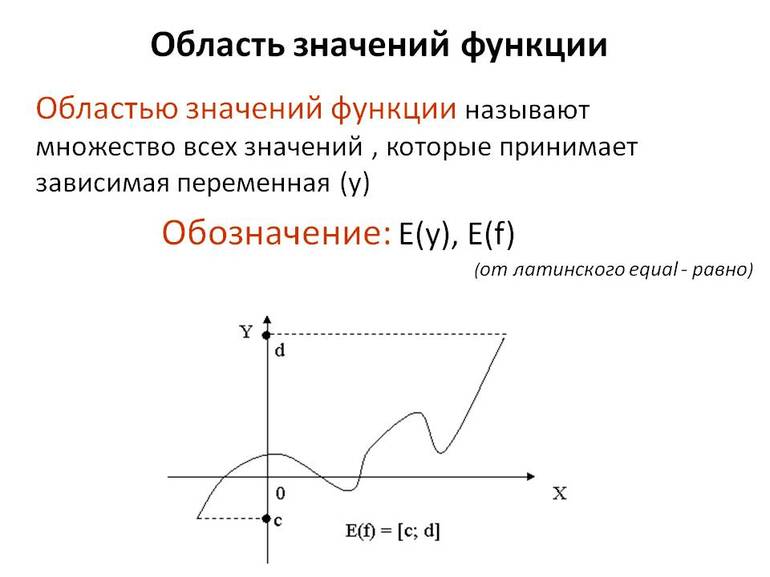
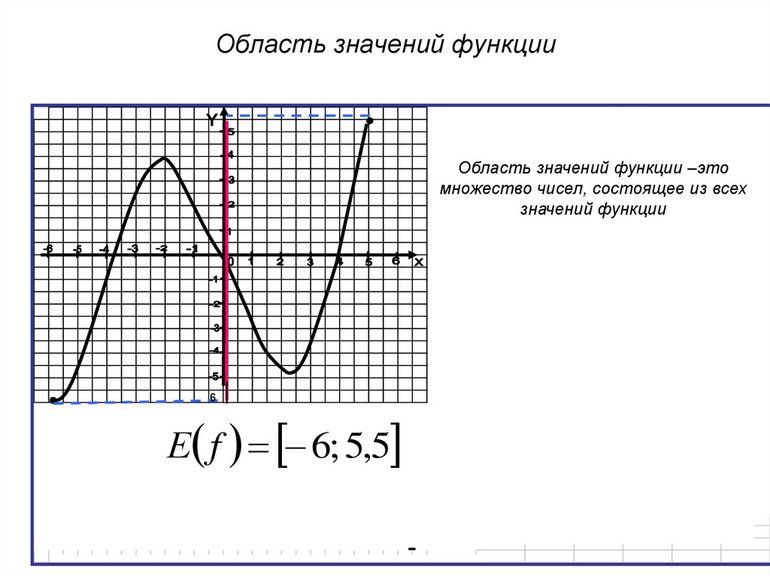
Областью значений числовой функции (ОЗФ) называется множество числовых значений, которые принимает функция y, если ее аргумент .

ОЗФ – это вспомогательная характеристика функции, которая вполне определяется после построения графика функции. До того, как график построен, ОЗФ может быть найдена только в отдельных случаях, когда это помогают сделать известные свойства основных элементарных функций, с помощью которых записана исследуемая функция. Для ОЗФ приняты также обозначения E(f) или E(y).

Пример (нахождение ООФ и ОЗФ)

Найти область определения и область значений в каждой из следующих функций:

1) ООФ: или ;

ОЗФ: , так как это сложная функция, полученная суперпозицией двух функций : и ;

2) ООФ: ;

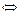
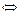
ООФ записана из ограничения по делению: на ноль делить нельзя;

ОЗФ можно найти только после построения графика функции;

3) ООФ: ;

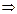
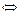
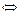
ООФ определена операцией извлечения корня квадратного, которая имеет смысл только для неотрицательных чисел;

ОЗФ: , так как корень квадратный принимает все неотрицательные значения, если ;

4) ООФ: ;

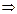
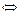
здесь ООФ учитывает ограничения операции логарифмирования (логарифмы существуют только от положительных чисел) и операции деления (на ноль делить нельзя);

ОЗФ определяется после построения графика функции;

5) , ООФ: ;

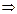
здесь ООФ записана по смыслу задания функции;

ОЗФ: – определена по графику функции ;

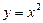
6) последовательность с общим членом может рассматриваться как функция натурального аргумента n, то есть ООФ: ;

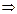
здесь ООФ записана по смыслу задания функции; ОЗФ: ;

7) ООФ: ; ОЗФ: .

Таким образом, в качестве ООФ и ОЗФ могут получиться любые множества: непрерывные или дискретные, бесконечные или конечные, в том числе может получиться пустое множество.

Дата добавления: 2015-10-19 ; просмотров: 13926 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

ООФ. ОЗФ. Определение свойств по графику. Построение графика по точкам

Ранее (в 6, 7 и начале 8 классов) вы познакомились с понятием функции, со свойствами и графиками некоторых функций и способами задания функций.

Если рассматривать графики реальных зависимостей, можно заметить, что всегда имеются две взаимосвязанные величины. С изменением первой величины меняются и значения второй. В таких ситуациях первую величину называют независимой, а другую зависимой. Так, например, с течением времени меняются рост человека, вес ребёнка, пройденная бегуном дистанция. В этих примерах время – независимая величина. Остальные величины, значения которых определяются значениями времени – зависимые. При построении графиков независимую величину всегда откладывают по горизонтальной оси, а зависимую – по вертикальной.

Функцией называется соответствие между множествами Х и Y, при котором каждому элементу множества Х соответствует единственный элемент множества Y.

Переменную х (элемент множества Х) называют независимой переменной или аргументом, а переменную у (элемент множества Y) – зависимой переменной. Говорят, что у является функцией от х. Если переменная у является функцией от переменной х, то используется запись y=f(x) (читается: «у равен f от х»). Если функция задана выражением с переменной х, то символом f(x) обозначается выражение, которым задаётся эта функция.

Если одновременно рассматриваются несколько функций, то для их обозначения используются и другие буквы латинского или греческого алфавитов. Например, буквы g, h, φ.

В формулу S=a 2 вместо переменной а можно подставить любое число. Однако если речь идёт о площади квадрата S как функции его стороны а, то областью определения этой функции является множество положительных чисел.

Область определения функции y=f(x) принято обозначать символом D(f) или D(y).

А область определения функции 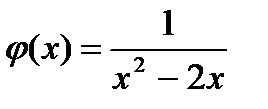так: D(y)= .

Все значения, которые принимает функция, называют областью значений функции.

Для области значений функции у=f(x) принято обозначение Е(f) или Е(у).

Значения аргумента, при которых функция у=f(x) обращается в нуль, называют нулями функции. Промежутки, в которых функция принимает только положительные или только отрицательные значения, называют промежутками знакопостоянства.

В различных областях науки и техники часто встречаются функции, которые называют квадратичными. Например, площадь квадрата у со стороной х, или если тело брошено вверх со скоростью v, то расстояние s от него до поверхности земли в момент времени t определяется формулой , где s₀ – расстояние от тела до поверхности земли в момент времени t=0.

В этих примерах рассмотрены функции вида y=ax 2 +bx+c.

Функция вида y=ax 2 +bx+c, где a, b, c – заданные действительные числа, а≠0, х – действительная переменная, называется квадратичной функцией.

Значение функции у=х 2 положительно при х≠0 и равно нулю при х=0. Можно увидеть, что парабола у=х 2 проходит через начало координат, а остальные точки параболы лежат выше оси абсцисс. Говорят, что парабола у=х 2 касается оси абсцисс в точке (0;0).

График функции у=х 2 симметричен относительно оси ординат. Таким образом, ось ординат является осью симметрии параболы. Точку пересечения параболы с её осью симметрии называют вершиной параболы. Для параболы у=х 2 вершиной является начало координат.

Говорят, что график функции у=2х 2 получается растяжением графика функции у=х 2 от оси Ох вдоль оси Оу в 2 раза.

В то же время можно заметить, что график функции получается сжатием графика функции у=х 2 к оси Ох вдоль оси Оу в 2 раза.

График функции у=ах 2 при любом а≠0 также называют параболой. При а>0 ветви параболы направлены вверх, а при a 0 во сколько раз увеличивается х, во столько же раз увеличивается и у.

Функции прямо пропорциональна числам, обратным значениям х. Здесь х стоит в знаменателе дроби. А мы уже знаем, что в дроби, чем больше знаменатель, тем меньше дробь и наоборот, чем меньше знаменатель, тем больше дробь. То есть функцию называют обратной пропорциональностью. Во сколько раз увеличивается х, во столько же раз уменьшается у, и во сколько раз уменьшается х, во столько же раз увеличивается у. При этом k≠0. Число k называют коэффициентом обратной пропорциональности.

Областью определения функции, заданной формулой , является множество действительных чисел, отличных от нуля, так как выражение имеет смысл при любых х, где х≠0.

Графиком функции обратная пропорциональность является гипербола. При k>0 график функции получается из графика функции путём его растяжения от оси х в k раз, если k>1, и его сжатия к оси х в раз, если 0

Источник

Общая информация

У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.

Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.

В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.

Основные понятия

Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».

Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.

Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.

Типы функций

Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:

Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.

Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.

Важные свойства

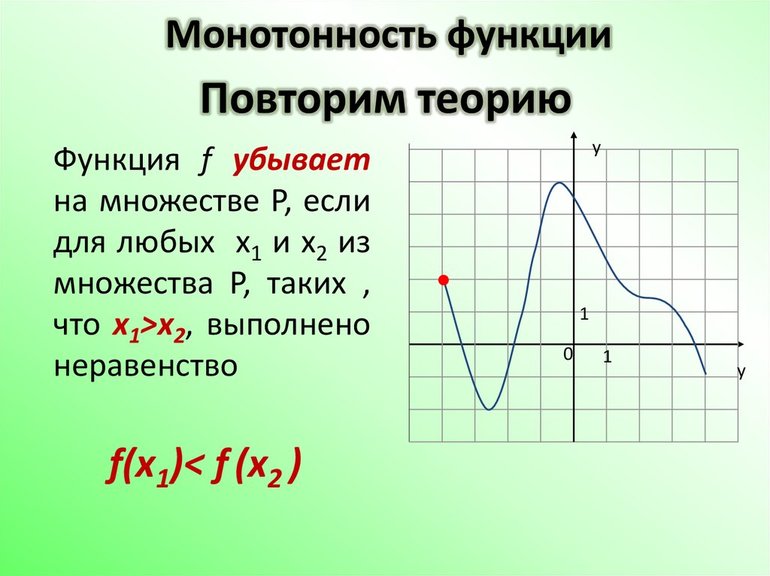
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:

Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.

Методы нахождения

Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:

Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.

Для каждого элемента

Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:

Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:

Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.

Оценочный способ

Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:

Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:

Производная, min и max

Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:

Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:

В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:

Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.

Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.

Источник