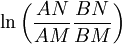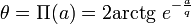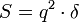Немецкий математик клейн утверждал что плоскость это внутренность некоторого круга

Проективное мышление. Геометрия Лобачевского в про

Проективное мышление. Геометрия Лобачевского в проективной форме
Впуклые щеки,
Выпуклые дырки,
Пьем коктейль по-русски,
Прямо из бутылки

. Так можно построить геометрию Лобачевского, если в качестве «абсолюта»выбрать невырожденную кривую второго порядка (или так называемую «овальную» кривую второго порядка).
Пусть на проективной плоскости задана овальная кривая второго порядка к(u), которую и будем считать абсолютом плоскости.
Эта кривая разделяет проективную плоскость на две области: внутреннюю и внешнюю. Точки внутренней области будем называть «собственными» или «действительными» точками. Точки самой овальной кривой, служащей абсолютом плоскости, назовем «несобственными» или «бесконечно удаленными». Наконец, точки внешней области будем называть «идеальными». «Собственные» точки и являются точками неевклидовой геометрии.
В качестве «прямых» нашей неевклидовой геометрии будут служить хорды овальной кривой (лежащие в ее внутренней области).
Так как концы этих хорд являются несобственными точками, то «прямые» неевклидовой геометрии являются открытыми отрезками. В указанной системе (собственных) точек и прямых могут быть сохранены те же отношения принадлежности, порядка и непрерывности, которые имеют место как в геометрии Евклида,
так и в геометрии Лобачевского.
Так, например, придавая понятию «принадлежность» обычный смысл, будем иметь: «две различные точки А и В определяют единственную принадлежащую им прямую (АВ)».
«Существуют три точки А, В и С, не лежащие на одной прямой», и т.д.
Далее, можно установить обычные как для геометрии Евклида, так и для геометрии Лобачевского отношения порядка. Точка на прямой разбивает последнюю на две части. Две точки А, В прямой устанавливают порядок точек на прямой и определяют отрезок АВ. Прямая делит неевклидову плоскость (под которой мы разумеем внутреннюю область овальной кривой к(u) на две части. Задание точки С, не лежащей на этой прямой, определяет соответствующую ей часть плоскости.
Сохраняется в рассматриваемом геометрии и свойство непрерывности точек на прямой, непрерывности всей неевклидовой плоскости.

Источник

Плоскость Лобачевского

Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского.

Евклидова аксиома о параллельных гласит:

через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её.

В геометрии Лобачевского, вместо неё принимается следующая аксиома:

через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Геометрия Лобачевского имеет обширные применения как в математике, так и в физике. Историческое её значение состоит в том, что её построением Лобачевский показал возможность геометрии, отличной от евклидовой, что знаменовало новую эпоху в развитии геометрии и математики вообще.

Содержание

История

Попытки доказательства пятого постулата

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в «Началах» Евклида). Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его из остальных постулатов Евклида.

Среди пытавшихся доказать были следующие учёные:

При этих попытках доказательства пятого постулата математики вводили некоторое новое утверждение, казавшееся им более очевидным.

Были предприняты попытки использовать доказательство от противного:

Наконец, стало возникать понимание о том, что возможно построение теории, основанной на противоположном постулате:

Создание неевклидовой геометрии

Лобачевский в работе «О началах геометрии» (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что V постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную, как и евклидова, и свободную от противоречий.

Одновременно и независимо к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше. Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций, и о его взглядах можно судить лишь по нескольким письмам и дневниковым записям. Например, в письме 1846 года астроному Г. Х. Шумахеру Гаусс так отзывается о работе Лобачевского:

Это сочинение содержит в себе основания той геометрии, которая должна была бы иметь место и притом составляла бы строго последовательное целое, если бы евклидова геометрия не была бы истинной… Лобачевский называет ее «воображаемой геометрией»; Вы знаете, что уже 54 года (с 1792 г.) я разделяю те же взгляды с некоторым развитием их, о котором не хочу здесь упоминать; таким образом, я не нашёл для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шёл я сам; оно выполнено Лобачевским мастерски в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение. [1]

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист этой теории.

Хотя геометрия Лобачевского развивалась как умозрительная теория и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно Лобачевский рассматривал её не как игру ума, а как возможную теорию пространственных отношений. Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации и тем полностью решён вопрос о её реальном смысле, логической непротиворечивости.

Утверждение геометрии Лобачевского

Лобачевский умер в 1856 году. Спустя несколько лет была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам Лобачевского. Появляются переводы их на французский и итальянский языки, комментарии видных геометров. Публикуется и труд Бойяи.

В 1868 году выходит статья Э. Бельтрами об интерпретациях геометрии Лобачевского. Бельтрами определил метрику плоскости Лобачевского и доказал, что она имеет всюду постоянную отрицательную кривизну. Такая поверхность тогда уже была известна — это псевдосфера Миндинга. Бельтрами сделал вывод, что локально плоскость Лобачевского изометрична участку псевдосферы (см. ниже). Окончательно непротиворечивость геометрии Лобачевского была доказана в 1871 году, после появления модели Клейна.

Вейерштрасс посвящает геометрии Лобачевского специальный семинар в Берлинском университете (1870). Казанское физико-математическое общество организует издание полного собрания сочинений Лобачевского, а в 1893 году столетие русского математика отмечается в международном масштабе.

Модели

Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.

Сам Лобачевский дал основы своей аналитической геометрии, и тем самым он уже фактически наметил такую модель. Он также заметил что орисфера в пространстве Лобачевского изометрична евклидовой плоскости, тем самым фактически предложил обратную модель. Тем не менее, само понятие о модели прояснилось в работах Клейна и других.

Псевдосфера

Итальянский математик Э. Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера. Если точкам и прямым на конечном куске плоскости Лобачевского сопоставлять точки и кратчайшие линии (геодезические) на псевдосфере и движению в плоскости Лобачевского сопоставлять перемещение фигуры по псевдосфере с изгибанием, то есть деформацией, сохраняющей длины, то всякой теореме геометрии Лобачевского будет отвечать факт, имеющий место на псевдосфере. При этом длины, углы, площади понимаются в смысле естественного измерения их на псевдосфере.

Однако здесь даётся только локальная интерпретация геометрии, то есть на ограниченном участке, а не на всей плоскости Лобачевского.

Модель Клейна

В 1871 году Клейн предложил первую полноценную модель плоскости Лобачевского.

В этой модели расстояние между точками A и B на хорде NM определяется через двойное отношение

Модель Пуанкаре

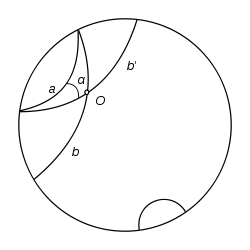
Позже Пуанкаре, в связи с задачами теории функций комплексного переменного дал другую модель. За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий относительно окружностей, дуги которых служат прямыми.

Модель Пуанкаре замечательна тем, что в ней углы изображаются обычными углами.

Поверхность постоянной отрицательной кривизны

Другое аналитическое определение геометрии Лобачевского состоит в том, что геометрия Лобачевского определяется как геометрия риманова пространства постоянной отрицательной кривизны. Это определение было фактически дано ещё в 1854 году Риманом и включало модель геометрии Лобачевского как геометрии на поверхностях постоянной кривизны. Однако Риман не связал прямо своих построений с геометрией Лобачевского, а его доклад, в котором он о них сообщил, не был понят и был опубликован лишь после его смерти (в 1868 году).

Содержание геометрии Лобачевского

Лобачевский строил свою геометрию, отправляясь от основных геометрических понятий и своей аксиомы, и доказывал теоремы геометрическим методом, подобно тому, как это делается в геометрии Евклида. Основой служила теория параллельных линий, так как именно здесь начинается отличие геометрии Лобачевского от геометрии Евклида. Все теоремы, не зависящие от аксиомы о параллельных, общи обеим геометриям и образуют так называемую абсолютную геометрию, к которой относятся, например, теоремы о равенстве треугольников. Вслед за теорией параллельных строились другие разделы, включая тригонометрию и начала аналитической и дифференциальной геометрии.

Приведём (в современных обозначениях) несколько фактов геометрии Лобачевского, отличающих её от геометрии Евклида и установленных самим Лобачевским.

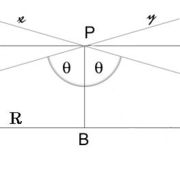
Через точку P, не лежащую на данной прямой R (см. рисунок), проходит бесконечно много прямых, не пересекающих R и находящихся с ней в одной плоскости; среди них есть две крайние x, y, которые и называются параллельными прямой R в смысле Лобачевского. В моделях Клейна (Пуанкаре) они изображаются хордами (дугами окружностей), имеющими с хордой (дугой) R общий конец (который по определению модели исключается, так что эти прямые не имеют общих точек).

Угол между перпендикуляром PB из P на R и каждой из параллельных (называемый углом параллельности) по мере удаления точки P от прямой убывает от 90° до 0° (в модели Пуанкаре углы в обычном смысле совпадают с углами в смысле Лобачевского, и потому на ней этот факт можно видеть непосредственно). Параллель x с одной стороны (а y с противоположной) асимптотически приближается к а, а с другой — бесконечно от неё удаляется (в моделях расстояния определяются сложно, и потому этот факт непосредственно не виден).

Для точки, находящейся от заданной прямой на расстоянии PB = a (см. рисунок), Лобачевский дал формулу для угла параллельности П(a) [2] :

Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы.

Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К любой из них можно восстановить перпендикуляры, которые не достигают другой прямой.

В геометрии Лобачевского не существует подобных, но неравных треугольников; треугольники равны, если их углы равны.

Линия равных расстояний от прямой не есть прямая, а особая кривая, называемая эквидистантой, или гиперциклом.

Предел окружностей бесконечно увеличивающегося радиуса не есть прямая, а особая кривая, называемая предельной окружностью, или орициклом.

Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или орисфера; замечательно, что на ней имеет место евклидова геометрия. Это служило Лобачевскому основой для вывода формул тригонометрии.

Длина окружности не пропорциональна радиусу, а растёт быстрее. В частности, в геометрии Лобачевского число π не может быть определено как отношение длины окружности к её диаметру.

Источник

Немецкий математик клейн утверждал что плоскость это внутренность некоторого круга

История создания геометрии Лобачевского одновременно является историей попыток доказать пятый постулат Евклида. Этот постулат представляет собой одну из аксиом, положенных Евклидом в основу изложения геометрии (см. Евклид и его «Начала»). Пятый постулат – последнее и самое сложное из предложений, включенных Евклидом в его аксиоматику геометрии. Напомним формулировку пятого постулата: если две прямые пересекаются третьей так, что по какую-либо сторону от нее сумма внутренних углов меньше двух прямых углов, то по эту же сторону исходные прямые пересекаются. Например, если на рис. 1 угол – прямой, а угол чуть меньше прямого, то прямые и непременно пересекаются, причем справа от прямой . Многие теоремы Евклида (например, «в равнобедренном треугольнике углы при основании равны») выражают гораздо более простые факты, чем пятый постулат. К тому же проверить на эксперименте пятый постулат довольно сложно. Достаточно сказать, что если на рис. 1 расстояние считать равным 1 м, а угол отличается от прямого на одну угловую секунду, то можно подсчитать, что прямые и пересекаются на расстоянии свыше 200 км от прямой .

Многие математики, жившие после Евклида, пытались доказать, что эта аксиома (пятый постулат) – лишняя, т.е. она может быть доказана как теорема на основании остальных аксиом. Так, в V в. математик Прокл (первый комментатор трудов Евклида) предпринял такую попытку. Однако в своем доказательстве Прокл незаметно для себя использовал следующее утверждение: два перпендикуляра к одной прямой на всем своем протяжении находятся на ограниченном расстоянии друг от друга (т.е. две прямые, перпендикулярные третьей, не могут неограниченно удаляться друг от друга, как линии на рис. 2). Но при всей кажущейся наглядной «очевидности» это утверждение при строгом аксиоматическом изложении геометрии требует обоснования. В действительности использованное Проклом утверждение является эквивалентом пятого постулата; иначе говоря, если его добавить к остальным аксиомам Евклида в качестве еще одной новой аксиомы, то пятый постулат можно доказать (что и сделал Прокл), а если принять пятый постулат, то можно доказать сформулированное Проклом утверждение.

Критический анализ дальнейших попыток доказать пятый постулат выявил большое число аналогичных «очевидных» утверждений, которыми можно заменить пятый постулат в аксиоматике Евклида. Вот несколько примеров таких эквивалентов пятого постулата.

1) Через точку внутри угла, меньшего, чем развернутый, всегда можно провести прямую, пересекающую его стороны, т.е. прямые линии на плоскости не могут располагаться так, как показано на рис. 3. 2) Существуют два подобных треугольника, не равных между собой. 3) Три точки, расположенные по одну сторону прямой на равном расстоянии от нее (рис. 4), лежат на одной прямой. 4) Для всякого треугольника существует описанная окружность.

Постепенно «доказательства» становятся все изощреннее, в них все глубже прячутся малозаметные эквиваленты пятого постулата. Допустив, что пятый постулат неверен, математики пытались прийти к логическому противоречию. Они приходили к утверждениям, чудовищно противоречащим нашей геометрической интуиции, но логического противоречия не получалось. А может быть, мы вообще никогда не придем на таком пути к противоречию? Не может ли быть так, что, заменив пятый постулат Евклида его отрицанием (при сохранении остальных аксиом Евклида), мы придем к новой, неевклидовой геометрии, которая во многом не согласуется с нашими привычными наглядными представлениями, но тем не менее не содержит никаких логических противоречий? Эту простую, но очень дерзкую мысль математики не могли выстрадать в течение двух тысячелетий после появления «Начал» Евклида.

Первым, кто допустил возможность существования неевклидовой геометрии, в которой пятый постулат заменяется его отрицанием, был К. Ф. Гаусс. То, что Гаусс владел идеями неевклидовой геометрии, было обнаружено лишь после смерти ученого, когда стали изучать его архивы. Гениальный Гаусс, к мнениям которою все прислушивались, не рискнул опубликовать свои результаты по неевклидовой геометрии, опасаясь быть непонятым и втянутым в полемику.

XIX в. принес решение загадки пятого постулата. К этому открытию независимо от Гаусса пришел и наш соотечественник – профессор Казанского университета Н. И. Лобачевский. Как и его предшественники, Лобачевский вначале пытался выводить различные следствия из отрицания пятого постулата, надеясь, что рано или поздно он придет к противоречию. Однако он доказал много десятков теорем, не обнаруживая логических противоречий. И тогда Лобачевскому пришла в голову догадка о непротиворечивости геометрии, в которой пятый постулат заменен его отрицанием. Лобачевский назвал эту геометрию воображаемой. Свои исследования Лобачевский изложил в ряде сочинений, начиная с 1829 г. Но математический мир не принял идеи Лобачевского. Ученые не были подготовлены к мысли о том, что может существовать геометрия, отличная от евклидовой. И лишь Гаусс выразил свое отношение к научному подвигу русского ученого: он добился избрания в 1842 г. Н. И. Лобачевского членом-корреспондентом Геттингенского королевского научного общества. Это единственная научная почесть, выпавшая на долю Лобачевского при жизни. Он умер, так и не добившись признания своих идей.

Рассказывая о геометрии Лобачевского, нельзя не отметить еще одного ученою, который вместе с Гауссом и Лобачевским делит заслугу открытия неевклидовой геометрии. Им был венгерский математик Я. Бойяи (1802-1860). Его отец, известный математик Ф. Бойяи, всю жизнь работавший над теорией параллельных, считал, что решение этой проблемы выше сил человеческих, и хотел оградить сына от неудач и разочарований. В одном из писем он писал ему: «Я прошел весь беспросветный мрак этой ночи и всякий светоч, всякую радость жизни в ней похоронил. она может лишить тебя всего твоего времени, здоровья, покоя, всего счастья твоей жизни. » Но Янош не внял предостережениям отца. Вскоре молодой ученый независимо от Гаусса и Лобачевского пришел к тем же идеям. В приложении к книге своего отца, вышедшей в 1832 г., Я. Бойяи дал самостоятельное изложение неевклидовой геометрии.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то в евклидовой геометрии равны и третьи углы (такие треугольники подобны). В геометрии Лобачевского не существует подобных треугольников. Более того, в геометрии Лобачевского имеет место четвертый признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то эти треугольники равны.

Разность между 180° и суммой углов треугольника в геометрии Лобачевского положительна; она называется дефектом этого треугольника. Оказывается, что в этой геометрии площадь треугольника замечательным образом связана с его дефектом: , где и означают площадь и дефект треугольника, а число зависит от выбора единиц измерения площадей и углов.

Пусть теперь – некоторый острый угол (рис. 5). В геометрии Лобачевского можно выбрать такую точку на стороне , что перпендикуляр к стороне не пересекается с другой стороной угла. Этот факт как раз подтверждает, что не выполняется пятый постулат: сумма углов и меньше развернутого угла, но прямые и не пересекаются. Если начать приближать точку к , то найдется такая «критическая» точка , что перпендикуляр к стороне все еще не пересекается со стороной , но для любой точки , лежащей между и , соответствующий перпендикуляр пересекается со стороной . Прямые и все более приближаются друг к другу, но общих точек не имеют. На рис. 6 эти прямые изображены отдельно; именно такие неограниченно приближающиеся друг к другу прямые Лобачевский называет в своей геометрии параллельными. А два перпендикуляра к одной прямой (которые неограниченно удаляются друг от друга, как на рис. 2) Лобачевский называет расходящимися прямыми. Оказывается, что этим и ограничиваются все возможности расположения двух прямых на плоскости Лобачевского: две несовпадающие прямые либо пересекаются в одной точке, либо параллельны (рис. 6), либо являются расходящимися (в этом случае они имеют единственный общий перпендикуляр, рис. 2).

На рис. 7 перпендикуляр к стороне угла не пересекается со стороной , а прямые симметричны прямым относительно . Далее, , так что – перпендикуляр к отрезку в его середине и аналогично – перпендикуляр к отрезку в его середине. Эти перпендикуляры не пересекаются, и потому не существует точки, одинаково удаленной от точек , т.е. треугольник не имеет описанной окружности.

На рис. 8 изображен интересный вариант расположения трех прямых на плоскости Лобачевского: каждые две из них параллельны (только в разных направлениях). А на рис. 9 все прямые параллельны друг другу в одном направлении (пучок параллельных прямых). Красная линия на рис. 9 «перпендикулярна» всем проведенным прямым (т.е. касательная к этой линии в любой ее точке перпендикулярна прямой, проходящей через ). Эта линия называется предельной окружностью, или орициклом. Прямые рассмотренного пучка являются как бы ее «радиусами», а «центр» предельной окружности лежит в бесконечности, поскольку «радиусы» параллельны. В то же время предельная окружность не является прямой линией, она «искривлена». И другие свойства, которыми в евклидовой геометрии обладает прямая, в геометрии Лобачевского оказываются присущими другим линиям. Например, множество точек, находящихся по одну сторону от данной прямой на данном расстоянии от нее, в геометрии Лобачевского представляет собой кривую линию (она называется эквидистантой).

НИКОЛАЙ ИВАНОВИЧ ЛОБАЧЕВСКИЙ
(1792-1856)

С 14 лет жизнь Н.И.Лобачевского была связана с Казанским университетом. Его студенческие годы приходились на благополучный период в истории университета. Было у кого учиться математике; среди профессоров выделялся М.Ф. Бартельс, сотоварищ первых шагов в математике К. Ф. Гаусса.

С 1814 г. Лобачевский преподает в университете: читает лекции по математике, физике, астрономии, заведует обсерваторией, возглавляет библиотеку. В течение нескольких лет он избирался деканом физико-математического факультета.

С 1827 г. начинается 19-летний период его непрерывного ректорства. Все надо было начинать заново: заниматься строительством, привлекать новых профессоров, менять студенческий режим. На это уходило почти все время.

Еще в первых числах февраля 1826 г. он передал в университет рукопись «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных», 11 февраля он выступил с докладом на заседании Совета университета. Собственно, речь шла не о доказательстве пятого постулата Евклида, а о построении геометрии, в которой имеет место его отрицание, т.е. о доказательстве его невыводимости из остальных аксиом. Вероятно, никто из присутствовавших не мог уследить за ходом мысли Лобачевского. Созданная комиссия из членов Совета несколько лет не давала заключения.

В 1830 г. в «Казанском вестнике» выходит работа «О началах геометрии», представляющая собой извлечение из доклада на Совете. Чтобы разобраться в ситуации, решили воспользоваться помощью столицы: в 1832 г. статью послали в Петербург. И здесь никто ничего не понял, работа была квалифицирована как бессмысленная. Не следует слишком сурово судить русских ученых: нигде в мире математики еще не были готовы воспринять идеи неевклидовой геометрии.

Ничто не могло поколебать уверенность Лобачевского в своей правоте. В течение 30 лет он продолжает развивать свою геометрию, пытается делать изложение более доступным, публикует работы по-французски и по-немецки.

Немецкую версию изложения прочитал Гаусс и, разумеется, понял автора с полуслова. Он прочитал его работы на русском языке и оценил их в письмах к ученикам, но публичной поддержки новой геометрии Гаусс не оказал.

Н. И. Лобачевский дослужился до высоких чинов, он был награжден большим числом орденов, пользовался уважением окружающих, но о его геометрии предпочитали не говорить, даже в те дни, когда Казань прощалась с ним. Прошло еще не менее двадцати лет, прежде чем геометрия Лобачевского завоевала права гражданства в математике.

Мы кратко коснулись только некоторых фактов геометрии Лобачевского, не упоминая многих других очень интересных и содержательных теорем (например, длина окружности и площадь круга радиуса здесь растут в зависимости от по показательному закону). Возникает убежденность, что эта теория, богатая очень интересными и содержательными фактами, в самом деле непротиворечива. Но эта убежденность (которая была у всех трех творцов неевклидовой геометрии) не заменяет доказательства непротиворечивости.

Чтобы получить такое доказательство, надо было построить модель. И Лобачевский это хорошо понимал и пытался ее найти.

Но сам Лобачевский этого уже не смог сделать. Построение такой модели (т.е. доказательство непротиворечивости геометрии Лобачевского) выпало на долю математиков следующего поколения.

В 1868 г. итальянский математик Э. Бельтрами исследовал вогнутую поверхность, называемую псевдосферой (рис. 10), и доказал, что на этой поверхности действует геометрия Лобачевского! Если на этой поверхности нарисовать кратчайшие линии («геодезические») и измерять по этим линиям расстояния, составлять из дуг этих линий треугольники и т.д., то оказывается, что в точности реализуются все формулы геометрии Лобачевского (в частности, сумма углов любого треугольника меньше 180°). Правда, на псевдосфере реализуется не вся плоскость Лобачевского, а лишь ее ограниченный кусок, но все же этим была пробита первая брешь в глухой стене непризнания Лобачевского. А через два года немецкий математик Ф. Клейн (1849-1925) предлагает другую модель плоскости Лобачевского.

Клейн берет некоторый круг и рассматривает такие проективные преобразования плоскости (см. Проективная геометрия), которые отображают круг на себя. «Плоскостью» Клейн называет внутренность круга , а указанные проективные преобразования считает «движениями» этой «плоскости». Далее, каждую хорду круга (без концов, поскольку берутся только внутренние точки круга) Клейн считает «прямой». Поскольку «движения» представляют собой проективные преобразования, «прямые» переходят при этих «движениях» в «прямые». Теперь в этой «плоскости» можно рассматривать отрезки, треугольники и т.д. Две фигуры называются «равными», если одна из них может быть переведена в другую некоторым «движением». Тем самым введены все понятия, упоминаемые в аксиомах геометрии, и можно производить проверку выполнения аксиом в этой модели. Например, очевидно, что через любые две точки проходит единственная «прямая» (рис. 11). Можно проследить также, что через точку , не принадлежащую «прямой» , проходит бесконечно много «прямых», не пересекающих . Дальнейшая проверка показывает, что в модели Клейна выполняются и все остальные аксиомы геометрии Лобачевского. В частности, для любой «прямой» (т.е. хорды круга ) и любой точки этой «прямой» существует «движение», переводящее ее в другую заданную прямую с отмеченной на ней точкой . Это и позволяет проверить выполнение всех аксиом геометрии Лобачевского.

Пуанкаре придумал фантастический мир, «жители» которого должны были бы принять геометрию Лобачевского из физических экспериментов. Для этого Пуанкаре предположил, что круг представляет собой неоднородную оптическую среду, в которой скорость света в точке равна расстоянию точки от границы круга . Тогда свет будет (в соответствии с принципом Ферма о минимальности времени движения по световой траектории) распространяться как раз по «прямым» рассмотренной модели. Свет не может за конечное время дойти до границы (поскольку там его скорость убывает до нуля), и потому этот мир будет восприниматься его «жителями» бесконечным, причем по своей метрике и свойствам совпадающим с плоскостью Лобачевского.

Впоследствии были предложены и другие модели геометрии Лобачевского. Этими моделями была окончательно установлена непротиворечивость геометрии Лобачевского. Тем самым было показано, что геометрия Евклида не является единственно возможной. Это оказало большое прогрессивное воздействие на все дальнейшее развитие геометрии и математики в целом.

А в XX в. было обнаружено, что геометрия Лобачевского не только имеет важное значение для абстрактной математики, как одна из возможных геометрий, но и непосредственно связана с приложениями математики к физике. Оказалось, что взаимосвязь пространства и времени, открытая в работах X. Лоренца, А. Пуанкаре, А. Эйнштейна, Г. Минковского и описываемая в рамках специальной теории относительности, имеет непосредственное отношение к геометрии Лобачевского. Например, в расчетах современных синхрофазотронов используются формулы геометрии Лобачевского.

Источник