перемещение частиц дисперсной фазы в электрическом поле к электроду называется
Перемещение частиц дисперсной фазы в электрическом поле к электроду называется
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
4.2 КОЛЛОИДНЫЕ СИСТЕМЫ
4.2.4 Двойной электрический слой и электрокинетические явления
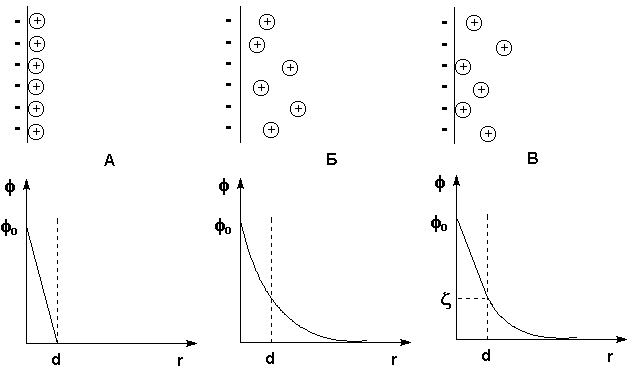
При рассмотрении строения мицеллы было показано, что на поверхности лиофобных коллоидов образуется двойной электрический слой. Первая теория строения ДЭС была развита Гельмгольцем и Перреном; в их представлении двойной электрический слой подобен плоскому конденсатору, внутренняя обкладка которого находится в твердой фазе, а внешняя – в жидкости параллельно поверхности ядра на расстоянии порядка диаметра иона. Потенциал электрического поля внутри ДЭС φ в этом случае линейно уменьшается с увеличением расстояния от поверхности r (рис. 4.12а).
Рис. 4.12 Строение ДЭС: а) – по Гельмгольцу и Перрену, б) – по Гуи и Чепмену, в) – по Штерну. Вверху – схема расположения противоионов, внизу – зависимость потенциала от расстояния
Рис. 4.13 Схема опыта по электрофорезу
Рис. 4.14 Схема опыта по электроосмосу
(IV.20)
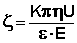
Обратные электрофорезу и электроосмосу электрокинетические явления (т.н. электрокинетические явления второго рода) называются соответственно потенциал седиментации и потенциал протекания. Потенциал седиментации (эффект Дорна) – возникновение разности потенциалов при вынужденном движении дисперсной фазы относительно неподвижной дисперсионной среды (например, под действием силы тяжести). Потенциал протекания (эффект Квинке) есть явление возникновения разности потенциалов при движении дисперсионной среды относительно неподвижной дисперсной фазы (например, при продавливании электролита через пористое тело).
Большая Энциклопедия Нефти и Газа
Перемещение частиц дисперсной фазы в электрическом поле к одному из электродов называют электрофорезом. [1]
Перемещение частиц дисперсной фазы в электрическом поле называется электрофорезом, а перемещение дисперсионной среды в этих условиях-электроосмосом. [3]
Электрофорезом называется перемещение частиц дисперсной фазы в электрическом поле. [4]
Такой конвективный перенос, осуществляемый под действием турбулентных пульсаций и часто называемый турбулентной диффузией, является основной причиной перемещения частиц дисперсной фазы от ядра потока к поверхности стенки трубы. [5]
Поведение суспензий в электрическом поле исследовали при 20 С в стеклянной ячейке с плоскими параллельными никелевыми электродами в интервале напряженностей до 12 5 кВ / см. Установлено, что в алифатических растворителях происходит перемещение частиц дисперсной фазы ( твердых углеводородов) в сторону катода, в то время как в ароматических растворителях эти же частицы перемещаются к аноду. В суспензиях твердых углеводородов, где дисперсионной средой являются полярные растворители ( МЭК, ацетон), явление электрофореза выражено слабо. Для таких систем характерна можэлектродная циркуляция, сопровождаемая агрегацией частиц. Эти электрокинетические явления в суспензиях твердых углеводородов объясняются существованием двойного электрического слоя на границе раздела фаз. Двойной электрофорез и межэлектродная циркуляция объясняются [115] поляризацией частиц твердой фазы и свойственны частицам, не имеющим заряда или находящимся в изоэлектрическом состоянии с мозаичным распределением участков с различным знаком заряда. Таким образом, у частиц дисперсной фазы как в полярной, так и в неполярной среде, отсутствует электрический заряд, а если он и есть, то весьма неустойчив. [6]
Он обнаружил, что если во влажную глину погрузить две стеклянные трубки, заполнить их водой и поместить в них электроды, то при пропускании постоянного тока происходит движение частичек глины к одному из электродов. Это явление перемещения частиц дисперсной фазы в постоянном электрическом поле было названо электрофорезом. В другом опыте средняя часть U-образной трубки, содержащей воду, была заполнена толченым кварцем, в каждое колено трубки помещен электрод и пропущен постоянный ток. [8]
Электрический заряд на коллоидных частицах возникает в результате процесса электролитической диссоциации вещества дисперсной фазы или вследствие избирательной адсорбции ионов из дисперсионной среды на поверхности частиц дисперсной фазы. Наличие заряда у коллоидных частиц можно обнаружить, пропуская через коллоидную систему постоянный электрический ток, под действием которого частицы перемещаются к электродам. Перемещение частиц дисперсной фазы под действием электрического тока называется электрофорезом. [9]
Последний аспект применения электрофореза наиболее интересен для очистки сточных вод от нерастворимых примесей. Электрофильтрование заключается в выделении из жидкостей дисперсной фазы за счет коагуляции, протекающей либо в объеме, либо на поверхностях электродов при наложении внешнего переменного или постоянного электрического поля. Внешнее электрическое поле обусловливает электрофоретическое перемещение частиц дисперсной фазы вдоль силовых линий и приводит к увеличению их концентрации у одного из электродов. Накопление частиц у электрода приводит к повышению скорости их коагуляции и соответственно увеличению скорости удаления дисперсной фазы из жидкости. [10]
Что такое электрофорез и электроосмос? Как объясняются эти явления?
Электрофорез и электроосмос
Наличие у частиц дисперсных систем электрического заряда было открыто еще в 1808 г. Процесс переноса частиц в электрическом поле получил название электрофореза. Процесс переноса жидкости при приложении разности потенциалов через пористую перегородку назван электроосмосом. Причем установлено, что количество жидкости, прошедшей через пористую перегородку пропорционально силе тока, и при постоянной силе тока не зависит от площади сечения или толщины перегородки.
При электрофорезе (рис. 3.5) в результате возникновения электрического поля между электродами, благодаря малому размеру частиц дисперсной фазы, происходит перенос отрицательно заряженной дисперсной фазы к положительному электроду. При электроосмосе (рис.З.б) пол влиянием электрического поля по капиллярам перегородки к отрицательному электроду передвигается положительно заряженная жидкость.
Почему при электродиализе используется только постоянный электрический ток?
Метод электродиализа использует:
1) электролитическую диссоциацию в воде молекул растворенных веществ на ионы;
2) направленное движение ионов в электрическом поле;
3) селективные свойства ионообменных мембран по отношению к ионам, имеющим заряды различных знаков.
Растворение солей в воде с образованием ионных пар происходит под воздействием диполей, образуемых молекулами воды в силу особенностей расположения в них атомов водорода и кислорода.
В постоянном электрическом поле ионы получают направленное движение согласно ориентации поля, при этом сохраняется принцип электронейтральности раствора в любой его точке.
Селективность ионообменных мембран, т.е. способность пропускать ионы с зарядом одного знака, обусловлена наличием в них фиксированных ионогенных групп, электрическое поле которых препятствует прохождению через мембрану ионов с зарядом того же знака, что и заряд иона фиксированного в полимерной матрице мембраны.
Электрофорез
Электрофорез — направленное перемещение частиц дисперсной фазы под действием приложенной разности потенциалов. Это явление наблюдается в седиментационно устойчивых дисперсных системах. При наложении на такую систему внешней разности потенциалов происходит разрыв ДЭС по плоскости скольжения, в результате чего частица получает заряд и перемещается к соответствующему электроду.
Приведенные выше уравнения Гельмгольца — Смолуховского справедливы для электрофореза, в частности для электрокинетического потенциала используется уравнение (4.9). Отличие состоит только в системе координат: в одном случае рассматривается скорость жидкости, в другом — скорость движения частиц, которую обычно определяют по смещению цветной границы.
Электрофорез наблюдают в U-образном сосуде (см. лабораторный практикум). В нижнюю часть сосуда наливают золь, сверху — контактную (боковую) жидкость, имеющую одинаковую (или немного большую) с золем электрическую проводимость. Наблюдают за изменением уровня золя в обоих коленах трубки и по скорости перемещения частиц дисперсной фазы определяют линейную скорость электрофореза Wq :
где S — путь, пройденный золем за время г (время электрофореза).
При электрофорезе отношение линейной скорости к напряженности
электрического поля 
называют электрофоретической подвижностью:
Напряженность электрического поля Е зависит от приложенной разности потенциалов на электродах U и расстояния между ними L:
Рассмотренные уравнения справедливы при допущениях: 1) частицы движутся в однородном электрическом поле; 2) частицы могут иметь любую форму и не проводят электрический ток; 3) толщина ДЭС много меньше размеров частиц золя.
Для расчета ^-потенциала частиц, находящихся в разбавленных водных растворах при 293 К, можно использовать простое соотношение:
в котором электрофоретическая подвижность и, выражена в(тогда
^-потенциал будет иметь размерность В). 
Несовпадение экспериментальных и теоретических значений объясняется релаксационным эффектом и электрофоретическим торможением.
Релаксационный эффект проявляется в нарушении симметрии диффузионного слоя вокруг частицы при относительном перемещении фаз в противоположные стороны.
Электрофоретическое торможение обусловлено сопротивлением движению частицы обратным потоком противоионов, которые увлекают за собой жидкость. В некоторых случаях несовпадение можно учесть введением поправок, иногда этим несовпадением можно пренебречь.
Скорость электрофореза зависит нс только от приложенного напряжения, но и от радиуса частиц и других факторов. Это можно учесть введением в уравнение (4.8) поправочного коэффициента к:
Поправочный коэффициент определяется экспериментально в каждом отдельном случае электрофореза.
Для примера рассмотрим данные по электрофорезу в суспензиях глин Трошковского, Никольского и Слюдянского месторождений, микрофотографии которых приведены на рис. 1.1.
Электрокинетический потенциал определяли методом подвижной границы при электрофорезе и рассчитывали по уравнению:
где S — путь; 
L — расстояние между электродами;
U — разность потенциалов между электродами;
tj — вязкость среды;
г — преимущественный радиус частицы, определяемый обычно по максимуму на кривой распределения частиц но размерам;
/(к г) — поправочная функция, учитывающая эффекты электрофоретического торможения и релаксации (табл. 4.1);
к — параметр Дебая, равный обратной величине плотной части двойного электрического слоя, то есть к = 1/6.
4.2.2. Элементарная теория электрокинетических явлений
Перемещение частиц дисперсной фазы в электрическом поле к одному из электродов, называемое электрофорезом, также является следствием нарушения электронейтральности двойного слоя. Без действия внешнего электрического поля двойной слой электронейтрален. При наложении разности потенциалов происходит разрыв двойного слоя по плоскости скольжения и частицы перемещаются тем быстрее, чем выше градиент потенциала. Частица, лишенная диффузной ионной оболочки, приобретает отрицательный заряд и будет перемещаться к положительному электроду. Измеренный по скорости перемещения частиц электрокинетический потенциал следует исправлять, учитывая сопротивление электроосмотического перемещения дисперсионной среды.
При определении электрокинетического потенциала методом электоосмоса делаются следующие предпосылки в соответствии с теорией Гельмгольца строения двойного ионного слоя.
2. Слой жидкости, непосредственно прилегающий к твердой поверхности, при электрокинетических явлениях остается неподвижным, тогда как все последующие слои перемещаются. Течение жидкости происходит в ламинарном режиме и описывается обычными уравнениями гидродинамики.
3. Стенка капилляра не проводит электрический ток и слой потенциалопределяющих ионов локализован, т.е. не может перемещаться по поверхности.
4. Внешняя разность потенциалов суммируется как аддитивная величина с перепадом потенциала в двойном слое. Это означает, что внешнее поле не деформирует двойного слоя, не нарушает его равновесия, хотя и обеспечивает непрерывное перемещение заряженного слоя жидкости вдоль поверхности.
Поскольку эта предпосылка предполагает постоянное восстановление равновесия в двойном слое в процессе электроосмоса, такая система может рассматриваться как конденсатор, пластины которого, находящиеся на расстоянии d, заряжены с поверхностной плотностью r. Данным значениям d и r соответствует разность потенциала между пластинами z. Поскольку толщина двойного слоя мала, то кривизной капилляра пренебрегают (считая, что слой плоский) и разрыв его в электрическом поле с градиентом потенциала Н= Е/l происходит по плоскости на расстоянии d от поверхности.
В таком случае напряжение сдвига в расчете на единицу площади поверхности, заставляющее жидкость двигаться,
. (1.4.11)
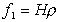
Это напряжение будет уравновешиваться сопротивлением ламинарного потока, т.е. силой трения
, (1.4.12)
. (1.4.13)
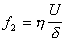
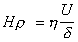
Учитывая, что для плоского конденсатора
, (1.4.14)
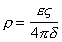
получаем для скорости течения
. (1.4.15)
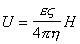
Количество жидкости, переносимое через капилляр, т.е. объемная скорость течения,
. (1.4.16)
. (1.4.17)
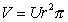
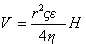
Естественно, что на практике не используют для измерений один капилляр, а изготавливают из непроводящего электрический ток материала мембрану толщиной l со множеством капилляров общим сечением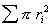 
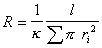
. Это сечение определяют по электрическому сопротивлению диафрагмы R, капилляры которой заполнены раствором с электропроводимостью k :
. (1.1.18)
В соответствии c законом Ома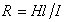 
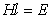
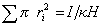
, где 
— разность потенциалов, приложенных к обеим сторонам мембраны, а I– сила тока.
. (1.4.19)
Заменяя в (1.4.16) 
на и используя (1.4.19), получаем
(1.4.20)
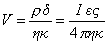
При использовании для расчетов формулы (1.4.20) следует учитывать, что величины h, kи e двойного слоя могут отличаться от величин, характерных для большого объема жидкости. С этой целью иногда вводится поправка на поверхностную проводимость ks, использовать которую предложил еще Смолуховский для учета конвективного потока ионов вдоль стенки капилляра, что возможно, выразив общую проводимость k узкого капилляра формулой
, (1.4.21)
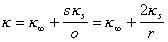
где s- периметр; o- сечение капилляра;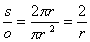 
.
Из уравнения (1.4.21) видно, что разность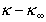 
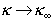
уменьшается с увеличением радиуса капилляра и 
, т.е. при определенных условиях электропроводность в пределах двойного слоя стремится к величине ее в объеме раствора.
Формула (1.4.20) применима при любом расположении капилляров в мембране, так как и электрический ток, и электроосмотический поток движутся параллельно стенкам капилляра.
Электроосмос не связан со структурой межфазной поверхности, но зависит от таких характеристик двойного слоя, как ks, e, d, r. Приведенные выше уравнения могут быть использованы и для расчета электрокинетического потенциала по скорости электрофореза. Механизм этого явления подобен механизму электроосмоса, но в данном случае неподвижной остается дисперсионная среда, а перемещаются частицы. Электрофоретическую скорость перемещения (подвижность) частиц Uef можно рассчитать, как U/H. Эта величина характеризует подвижность коллоидной частицы при электрофорезе. В принципе, она аналогична подвижности ионов в электрическом поле, поэтому
Эта формула не учитывает влияния ионной атмосферы на электрофоретическую подвижность и формы частиц. Более правильно следует записать ее, как предложил Генри (1931 г.),
(1.4.23)
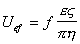
где f- сила электрофоретического торможения, которая зависит от радиуса частиц и радиуса ионной атмосферы (фактора Дебая) k. Для цилиндрических частиц, ось которых ориентирована по направлению электрического поля, f = 1/4. Если ось перпендикулярна к полю, f = 1/8. Для сферических частиц f = 1/6 и стремится к 1/4 при больших значениях kr. Все это справедливо для частиц, не проводящих электрический ток. Кроме того, при утолщении двойного ионного слоя становится некорректным рассмотрение гидродинамических и электрических явлений порознь внутри и вне двойного слоя, как это делал Смолуховский. Потенциал течения способен возникать в том случае, если при воздействии силового механического поля течение жидкости увлекает ионы диффузионной обкладки двойного слоя, так что вдоль стенки капилляра возникает стационарный поток ионов. Если вдоль капилляра существует градиент давления dP/dl, где l – длина капилляра, то возникает течение, которое в соответствии с законом Пуазейля при x 2 слоя, движущихся на расстоянии d со скоростью Ud.:
. (1.4.26)
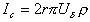
Перенос электрического заряда вызывает разность потенциалов E=Hl на концах капилляра, которая, в свою очередь, вызывает протекание нарастающего тока проводимости через раствор с сопротивлением R. Когда ток проводимости становится равным конвективному потоку, разность потенциалов приобретает постоянное стационарное значение, равное потенциалу течения DVst. Согласно закону Ома
при 
. (1.4.27)
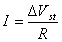
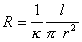
Приравнивая (1.4.26) и (1.4.27) и подставляя (1.4.25), получаем
. (1.4.28)
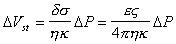
В этом выражении для поверхностной плотности заряда использовалось выражение (1.4.14). Формула (1.4.28) справедлива и для случая пористой перегородки с капиллярами произвольной формы. Если сопоставить результаты измерения потенциала течения и электроосмотической скорости для одной и той же системы, то получим
. (1.4.29)
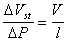
Седиментационный поток частиц относительно неподвижной жидкости возбуждает конвективный поток ионов диффузионного двойного слоя. Поле, которое при этом возникает, препятствует этому перемещению. Поэтому, по аналогии с приведенным выше потенциалом течения, получим уравнение для расчета потенциала седиментации Esed. Скорость седиментации сферических частиц в соответствии с законом Стокса
, (1.4.30)
. (1.4.31)
. (1.4.32)
. (1.4.33)
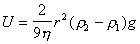
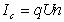
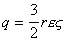
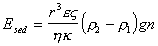
Уравнение (1.4.33) справедливо для седиментации твердых частиц. При обратной седиментации при расчете потенциала для эффекта Дорна всплывающих газовых пузырьков или капелек жидкости необходимо учитывать сопутствующий электрокинетическим явлениям эффект диффузии ионов. При движении твердых частиц в растворе электролита возникает разность концентраций между полюсами по направлению движения частиц и проявляется диффузионный потенциал. Только при равенстве коэффициентов диффузии катионов и анионов в классические уравнения не вводятся поправки. Во всех остальных случаях уравнения должны быть откорректированы.