Номинальный размер это что такое

Номинальный размер

Номинальный размер – изд. стр.-дор. размер изделия, установленный изготовителем и соответствующий фактическому размеру изделия в пределах допустимых отклонений.

Рубрика термина: Асфальт

Полезное

Смотреть что такое «Номинальный размер» в других словарях:

номинальный размер — Нормируемый размер изделия, фактический размер которого соответствует границам допускаемых отклонений. [ГОСТ 31360 2007] Тематики строительные конструкции … Справочник технического переводчика

Номинальный размер — размер, относительно которого определяются предельные размеры и допустимые отклонения. Служит началом отсчета отклонений. Используется, напр., при определении форматного ряда полиграфической продукции, отдельных изданий и полос (страниц) … Реклама и полиграфия

номинальный размер — 3.5 номинальный размер (общая высота, диаметр): По ГОСТ 17527. Источник: ГОСТ Р 52327 2005: Тара стеклянная для продуктов детского питания. Технические условия … Словарь-справочник терминов нормативно-технической документации

номинальный размер DN — 3.2 номинальный размер DN: Числовое обозначение размера элементов трубопровода, приблизительно равное производственным размерам, в миллиметрах. Источник … Словарь-справочник терминов нормативно-технической документации

номинальный размер DN/ID — 3.3 номинальный размер DN/ID: Номинальный размер, относящийся к внутреннему диаметру. Источник: ГОСТ Р 54475 2011: Трубы полимер … Словарь-справочник терминов нормативно-технической документации

номинальный размер DN/OD — 3.4 номинальный размер DN/OD: Номинальный размер, относящийся к наружному диаметру. Источник: ГОСТ Р 54475 2011: Трубы полимерны … Словарь-справочник терминов нормативно-технической документации

номинальный размер — vardinis matmuo statusas T sritis Standartizacija ir metrologija apibrėžtis Matmuo, kurio atžvilgiu nustatomi ribiniai matmenys ir kuris yra leidžiamųjų nuokrypų atskaitos pradžia. atitikmenys: angl. nominal dimension vok. Nennmaß, n rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

номинальный размер — vardinis matmuo statusas T sritis fizika atitikmenys: angl. nominal dimension vok. Nennmaß, n rus. номинальный размер, m pranc. dimension nominale, f … Fizikos terminų žodynas

Номинальный размер — размер, относительно которого определяются предельные размеры. Служит началом отсчета отклонений. Используется, например, при определении форматного ряда полиграфической продукции … Краткий толковый словарь по полиграфии

номинальный размер элемента — Размер элемента в знаке символа, соответствующий установленному Источник: ГОСТ 30721 2000: Автоматическая идентификация. Кодирование штриховое. Термины и определения … Словарь-справочник терминов нормативно-технической документации

Источник

Номинальным размером

3. Номинальным размером называется основной размер, определенный исходя из функционального назначения детали и служащий началом отсчета отклонений. Общий для отверстия и вала, составляющих соединение, номинальный размер называется номинальным размером соединения.

2. Номинальные размеры должны выбираться по ГОСТ 6636.

Смотреть что такое «Номинальным размером» в других словарях:

ГОСТ 25346-89: Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений — Терминология ГОСТ 25346 89: Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений оригинал документа: 1.1.19. Вал термин, условно применяемый для обозначений наружных элементов… … Словарь-справочник терминов нормативно-технической документации

отклонение — 1.3.2.28 отклонение: Максимальное отклонение от температурной уставки, указанное изготовителем. Источник: ГОСТ Р 51983 2002: Устройства многофункциона … Словарь-справочник терминов нормативно-технической документации

ГОСТ 7713-62: Допуски и посадки. Основные определения — Терминология ГОСТ 7713 62: Допуски и посадки. Основные определения оригинал документа: 4. Действительным размером называется размер, полученный в результате измерения с допустимой погрешностью. Определения термина из разных документов:… … Словарь-справочник терминов нормативно-технической документации

Допуск — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия

Допуск (техника) — Допуск разность между наибольшим и наименьшим предельными значениями (размеров, массовой доли, массы), задаётся на геометрические размеры деталей, механические, физические и химические свойства. Назначается (выбирается) исходя из технологической… … Википедия

Допуск (машиностроение) — Допуск разность между наибольшим и наименьшим предельными значениями (размеров, массовой доли, массы), задаётся на геометрические размеры деталей, механические, физические и химические свойства. Назначается (выбирается) исходя из технологической… … Википедия

Квалитет — Допуск разность между наибольшим и наименьшим предельными значениями (размеров, массовой доли, массы), задаётся на геометрические размеры деталей, механические, физические и химические свойства. Назначается (выбирается) исходя из технологической… … Википедия

твердые частицы — 3.1 твердые частицы (particulate matter): Нерастворимые частицы, остающиеся на фильтровальной бумаге, номинальным размером 10 мкм. Источник: ГОСТ Р ИСО 15859 1 2010: Системы космические. Характеристики, отбор проб и методы анализа текучих сред.… … Словарь-справочник терминов нормативно-технической документации

Щебень — 3.1. Щебень из плотных горных пород и щебень из гравия, щебень из шлаков, входящие в состав смесей, песок природный и из отсевов дробления горных пород, минеральный порошок должны соответствовать требованиям ГОСТ 9128 97, пункт 5.15. 3.2.… … Словарь-справочник терминов нормативно-технической документации

Щебень из плотных горных пород для балластного слоя железнодорожного пути — неорганический зернистый сыпучий материал с номинальным размером зерен от 25 до 60 мм, получаемый дроблением изверженных горных пород с последующим рассевом продуктов дробления. Источник: ГОСТ 7392 2002 … Словарь-справочник терминов нормативно-технической документации

Источник

Основные понятия и определения: номинальный размер, предельные размеры, предельные отклонения, допуск, посадка, зазор, натяг

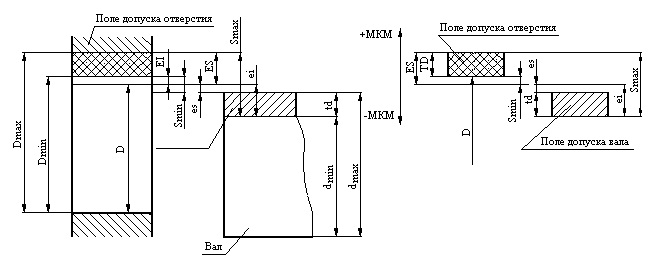
1. Основные понятия и определения: номинальный размер, предельные размеры, предельные отклонения, допуск, посадка, зазор, натяг. Дать схему расположения полей допусков отверстия и вала для переходной посадки. Обозначить на ней указанные понятия и дать формулы связи между ними.

Размеры подразделяются на истинные, действительные, предельные, номинальные.

Истинный размер – некоторая абсолютная величина, к которой мы стремимся, повышая качество изделий.
Действительный размер – размер элемента установленный измерениями с допустимой погрешностью.

На практике вместо истинного размера используют действительный размер.

Номинальный размер – размер, относительно которого определяют предельные размеры и который служит также началом отсчета отклонений. Для сопрягаемых деталей номинальный размер является общим. Он определяется расчетами на прочность, жесткость и т. д., округляется до наибольшего значения с учетом «нормальных линейных размеров».

Нормальные линейные размеры.

Нормальные линейные размеры применяются с целью уменьшения разнообразия назначаемых конструктором размеров со всеми вытекающими преимуществами (сужением сортамента материалов, номенклатуры мерного, режущего и измерительного инструмента и т. д.).

Ряды нормальных линейных размеров – это геометрические прогрессии со знаменателем. В ряду пять значений. Эти соотношения сохраняются для различных числовых интервалов.

Первый ряд Ra 5 g = 10 = 1,6

100; 160; 250; 400; 630

Второй ряд Ra 10 g = 10 = 1,25

1; 1.25; 1.6; 2.0; 2.5; 3.2; 4.0; 5.0; 6.3; 8.0

Каждый следующий ряд включает в себя члены предыдущего.

Третий ряд Ra 20 g = 10 = 1,12

Четвертый ряд Ra 40 g = 10 = 1,06

При выборе номинальных размеров, предшествующий ряд предпочтительнее последующего.

Номинальный размер обозначается для отверстий D и вала d.

Предельные размеры: два предельно допустимых размера элемента, между которыми должен находится, или которым может быть равен действительный размер.

Наибольший предельный размер: наибольший допустимый размер элемента, номинальный наоборот.

Dmax, Dmin, dmax, dmin

С целью упрощения обозначения предельных размеров на чертежах введены предельные отклонения от номинального размера.

Верхнем предельным отклонением ES(es) называется алгебраическая разность между наибольшим предельным размером и номинальным размером.

EI = dmax –D для отверстия

es = dmax – d для вала

Нижним предельным отклонением EI(ei)называется алгебраическая разность между наименьшем предельным отклонением и номинальным размером.

EI = dmin – D для отверстия

Ei = dmin – d для вала

Действительным отклонением называется алгебраическая разность между действительным и номинальным размерами.

Значения отклонений могут быть положительным и отрицательным числом.

На машиностроительных чертежах линейные, номинальные, предельные размеры, а также отклонения проставляют в миллиметрах.

Угловые размеры и их предельные отклонения проставляют в градусах, минутах, секундах с указанием единиц.

При равенстве абсолютных величины отклонений 42 + 0,2; 120 + 2

Отклонение, равное нулю на чертежах не проставляют, наносят только одно отклонение – положительное вверху, отрицательное внизу.

Отклонение записывается до последней значащей цифры. Для производства важнее не отклонение, а ширина интервала, который называется допуском.

Допуск – разность между наибольшим и наименьшим предельными размерами или абсолютная величина алгебраической разности между верхним и нижним отклонениями.

TD = Dmax – Dmin = ES – EI

Допуск всегда положителен, он определяет допускаемое поле рассеивания действующих размеров деталей в партии, которые признаются годными, т. е. он определяет заданную точность изготовления.

Назначения рационального допуска – важная задача, сочетающая в себе экономические и качественные требования производства.

С увеличением допуска качество изделий, как правило, ухудшается, зато стоимость изготовления падает.

Пространство на схеме, ограниченное линиями верхнего и нижнего отклонений называется полем допуска.

Упрощенное изображение полей допусков, при котором схемы отверстий и вала отсутствуют.

Пример: Построить схему расположения полей допусков для валов с номинальным размером 20 и предельными отклонениями

1. es = + 0,02 2. es = + 0,04

T1 = + 0,0,01) = 0,03 мм T2 = 0,04 – 0,01 = 0,03 мм

Сравнительная точность деталей 1 и 2 одинакова. Критерий точности – допуск T1 = T2, но поля допусков разные, т. к. они отличаются расположением относительно номинального размера.

Обозначение отклонений на чертежах.

dmax = d + es

С понятием взаимозаменяемости связано понятие о годности детали. Всякая реальная деталь будет годной если:

При методе непосредственной оценки (НО) настройку прибора на нуль производят по базовой поверхности прибора. Под действием различных факторов (изменения температуры, влажности, вибраций и т. д.) может произойти смешение нуля. Поэтому периодически необходимо производить проверку и соответствующую регулировку.

Метод сравнения – измеряемую величину сравнивают с величиной, воспроизводимой мерой. При измерении методом сравнения с мерой результатом наблюдения является отклонение измеряемой величины от значения меры. Значение измеряемой величины от значения меры. Значение измеряемой величины получают алгебраическим суммированием значения меры и отклонения от этой меры, определенного по показанию прибора.

Метод непосредственной оценки Метод сравнения

Выбор метода измерения определяется соотношением между диапазоном показаний средства измерения и значением измеряемой величины.

Если диапазон меньше измеряемой величины, то используют метод сравнения.

Метод сравнения используют при измерении, контроле деталей в массовом и серийном производствах, т. е. когда нет частых переналадок измерительного прибора.

1. Характеристики системы допусков и посадок гладких цилиндрических соединений: нормальная температура, единица допуска, квалитеты, формула допусков, интервалы диаметров и ряды допусков.

2. Параметры шероховатости Ra, Rz, Rmax. Нормирование и примеры обозначения на чертеже шероховатости поверхности с использованием этих параметров.

3. Приведенный диаметр наружной резьбы. Суммарный допуск среднего диаметра резьбы. Условие годности наружной резьбы по среднему диаметру. Пример обозначения точности резьбы болта на чертеже.

1.Характеристики системы допусков и посадок гладких цилиндрических соединений: основные отклонения валов и отверстий и схемы расположения, поле допуска и его обозначение, предпочтительные поля допусков и схемы их расположения.

2. Параметры шероховатости, S и Sm. Нормирование и примеры обозначения на чертеже шероховатости поверхности с использованием этих параметров.

3. Классификация зубчатых передач по функциональному назначению. Примеры обозначения точности зубчатых колес.

1. Три типа посадок, схема расположения полей допусков и характеристики этих посадок. Примеры обозначения посадок на чертежах.

2. Параметр шероховатости tp. Нормирование и примеры обозначения на чертеже шероховатости поверхности с использованием этого параметра.

3. Погрешности измерения. Классификация составляющих погрешности измерения по причинам их возникновения.

1. Три типа посадок в системе отверстия. Схемы расположения полей допусков и примеры обозначения посадок в системе отверстия на чертеже.

2. Отклонения формы цилиндрических поверхностей, их нормирование и примеры обозначения на чертежах допусков формы цилиндрических поверхностей.

3. Приведенный средний диаметр внутренней резьбы. Суммарный допуск среднего диаметра резьбы. Условие годности внутренней резьбы по среднему диаметру. Пример обозначения точности гайки на чертеже.

1. Три типа посадок в системе вала. Схемы расположения полей допусков и примеры обозначения посадок в системе вала на чертеже.

2. Отклонения формы плоских поверхностей. Их нормирование и примеры обозначения на чертеже допусков формы плоских поверхностей.

3. Нормирование точности зубчатых колес и передач. Принцип комбинирования ном точности. Примеры обозначения точности зубчатых колес.

1.Посадки с зазором. Схемы расположения полей допусков в системе отверстия и системе вала. Применение посадок с зазором и примеры обозначения на чертежах.

2. Принципы нормирования отклонений формы и обозначение допусков формы на чертежах. Отклонения формы поверхностей, основные определения.

3. Случайные погрешности измерения и их оценка.

1. Посадки с натягом. Схемы расположения полей допусков в системе отверстия и вала. Применение посадок с натягом и примеры обозначения на чертежах.

2. высотные параметры шероховатости поверхности. Нормирование и примеры обозначения на чертежах шероховатости поверхности с использованием высотных параметров.

3. Нормирование точности метрической резьбы. Примеры обозначения на чертежах посадок резьбовых соединений с зазором.

1.Переходные посадки. Схемы расположения полей допусков в системе вала и отверстия. Применение переходных посадок и примеры обозначения на чертеже.

2. Шаговые параметры шероховатости поверхности. Нормирование и примеры обозначения на чертеже шероховатости поверхности с использованием шаговых параметров.

3. Кинематическая точность зубчатых колес и передач, ее нормирование. Пример обозначения точности зубчатого колеса для отсчетных передач.

1.Система отверстия. Схема расположения полей допусков трех типов посадок в системе отверстия. Примеры обозначения посадок в системе отверстия на чертеже.

2. Параметр формы шероховатости. Нормирование и примеры обозначения на чертежах шероховатости поверхности с использованием параметра формы.

3. Систематические погрешности измерения, способы их обнаружения и устранения.

1.Система вала. Схема расположения полей допусков трех типов посадок в системе вала. Примеры обозначения посадок в системе вала на чертежах.

2. Обозначение на чертежах шероховатости поверхности. Примеры обозначения шероховатости поверхности, вид обработки, который конструктором не устанавливается; обрабатываемой со снятием слоя материала; сохраняемой в состоянии поставки; обрабатываемой без снятия слоя материала.

3. Основные отклонения диаметров резьбы для посадок с зазором и схемы их расположения. Примеры обозначения посадок метрической резьбы на чертежах.

1. Посадки с зазором. Схемы расположения полей допусков посадок с зазором в системе отверстия. Показать, как изменятся Smax, Smin, Sm, Ts при изменении допусков соединяемых деталей на один квалитет. Примеры обозначения на чертежах посадок с зазором в системе отверстия.

2. Отклонения расположения поверхностей, их нормирование и примеры обозначения на чертежах допусков расположения поверхностей.

3. Контакт зубьев в передаче и его нормирование. Пример обозначения точности зубчатого колеса для силовой передачи.

1. Посадки с натягом, схемы расположения полей допусков посадок с натягом в системе отверстия. Показать, как изменятся Nmax, Nmin, Nm, TN при изменении допусков соединяемых деталей на один квалитет. Примеры обозначения на чертежах посадок с натягом в системе отверстия.

2. Шероховатость поверхности, причины ее возникновения. Нормирование шероховатости поверхности и примеры обозначения на чертежах.

3. Выбор средств измерения.

1.Переходные посадки, схемы расположения полей допусков переходных посадок в системе отверстия. Показать, как изменятся Smax, Smin, Sm(Nm), TSN при изменении допусков соединяемых деталей на один квалитет. Примеры обозначения на чертежах переходных посадок в системе отверстия.

2. Отклонения от соосности и пересечение осей, их нормирование и примеры обозначения на чертежах.

3. Нормирование и обозначение на чертежах точности наружной резьбы.

1. Посадки с зазором. Схемы расположения полей допусков посадок с зазором в системе вала. Показать, как изменятся Smax, Smin, Sm, Ts при изменении допусков соединяемых деталей на один квалитет. Примеры обозначения на чертежах посадок с зазором в системе вала.

2. Отклонение от симметричности и позиционное отклонение, их нормирование и примеры обозначения на чертежах.

3. Плавность работы зубчатых колес и передач, ее нормирование. Пример обозначения точности зубчатого колеса для скоростной передачи.

1. Посадки с натягом, схемы расположения полей допусков посадок с натягом в системе вала. Показать, как изменятся Nmax, Nmin, Nm, TN при изменении допусков соединяемых деталей на один квалитет. Примеры обозначения на чертежах посадок с натягом в системе вала.

2. Радиальное и торцевое биения, их нормирование и примеры обозначения на чертеже.

3. Математическая обработка результатов наблюдения. Форма представления результата измерения.

1. Переходные посадки, схемы расположения полей допусков переходных посадок в системе вала. Показать, как изменятся Smax, Smin, Sm(Nm), TSN при изменении допусков соединяемых деталей на один квалитет. Примеры обозначения на чертежах переходных посадок в системе вала.

2.Параметры шероховатости Ra, Rz, Rmax. Примеры применения этих параметров для нормирования шероховатости поверхности.

3. Принципы обеспечения взаимозаменяемости резьбовых соединений. Примеры обозначения точности резьбовых соединений на чертежах.

1.Посадки с зазором и их расчет (выбор). Обозначение посадок с зазором на чертежах. Примеры применения предпочтительных посадок с зазором.

2. Параметры шероховатости поверхности Sm и S. Примеры применения этих параметров для нормирования шероховатости поверхности.

3.Погрешность измерения и ее составляющие. Суммирование погрешностей при прямых и косвенных измерениях.

1. Посадки с натягом и их расчет (выбор). Обозначение посадок с натягом на чертежах. Примеры применения предпочтительных посадок с натягом.

2. Параметр шероховатости tp и примеры его применения для нормирования шероховатости поверхности.

3. Виды сопряжений зубьев колес в передаче. Примеры обозначения точности зубчатых колес.

1. Переходные посадки и их расчет (выбор). Обозначение переходных посадок на чертежах. Примеры применения предпочтительных переходных посадок.

2. Принцип предпочтительности, ряды предпочтительных чисел.

3. Понятие о контроле, контроль предельными калибрами. Схемы расположения полей допусков калибров для контроля отверстий. Расчет и обозначение на чертежах исполнительных размеров калибров-пробок.

1. Посадки подшипников качения в соединениях с корпусом и валом и схемы расположения полей допусков. Примеры обозначения посадок подшипников качения на чертеже.

2. Понятие о взаимозаменяемости и ее видах.

3. Нормирование и обозначение на чертежах точности внутренней резьбы.

1. Выбор посадок подшипников качения в зависимости от вида нагружения колец и класса точности подшипника. Примеры обозначения посадок подшипников качения на чертежах.

2. Понятие о стандартизации. Государственная система стандартизации. Категории и виды стандартов.

3. Понятие о контроле, контроль предельными калибрами. Схемы расположения полей допусков калибров для контроля валов. Расчет и обозначение на чертежах исполнительных размеров калибров-скоб.

1. Схемы расположения полей допусков в соединениях подшипников качения с валом и корпусом. Примеры обозначения посадок подшипников качения на чертежах.

2. Научно-технические принципы стандартизации. Роль стандартизации в обеспечении качества продукции.

3. Боковой зазор в зубчатых передачах и его нормирование. Примеры обозначения точности зубчатых колес.

1.Система отверстия. Схема расположения полей допусков трех типов посадок в системе отверстия. Примеры обозначения посадок в системе отверстия на чертеже.

2. Унификация, симплификация, типизация и агрегатирование и их роль в повышении качества машин и приборов.

3. Диаметральные компенсации погрешностей шага и угла профиля резьбы. Пример обозначения точности резьбы болта с длинной свинчивания, отличающейся от нормальной.

1.Система вала. Схема расположения полей допусков трех типов посадок в системе вала. Примеры обозначения посадок в системе вала на чертежах.

2. Качество продукции и его основные показатели. Аттестация качества продукции.

3. Поле допуска наружной резьбы и его обозначение. Предельные контуры наружной резьбы и условие годности.

Источник

21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения.

21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения. 21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения.

Поверхности, размеры, отклонения и допуски. Поверхности деталей бывают сопрягаемыми и несопрягаемыми, или свободными. При этом они могут быть цилиндрическими, плоскими, коническими, эвольвентными, сложными (шлицевые, винтовые) и др. Со-прягаемыми называют поверхности, по которым детали соединяются в сборочные единицы, а сборочные единицы — в механизмы. Несопрягаемыми, или свободными, — конструктивно необходимые поверхности, не предназначенные для соединения с поверхностями других деталей.

Внутренние цилиндрические поверхности, а также внутренние поверхности с парал-лельными плоскостями (отверстия в ступицах, шпоночные пазы и пр.) являются охватывающими (их условно называют отверстиями; диаметры отверстий обозначают буквой D). Наружные отверстия (цилиндрическая поверхность вала, боковые грани шпонок) являются охватываемыми (их условно называют валами и обозначают буквой d).

Размеры — это числовое значение линейной величины (диаметра, длины и т.д.), они делятся на номинальные, действительные и предельные. В машино и приборостроении все размеры в технической документации задают и указывают в миллиметрах.

Номинальный размер (D) — размер, относительно которого определяют предельные размеры и отсчитывают отклонения. Номинальные размеры являются основными размерами деталей или их соединений. Сопрягаемые поверхности имеют общий номинальный размер.

Действительный размер (Dr, dr) — размер, установленный измерением с допустимой погрешностью. Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерения, а следовательно, и выбор измерительных средств необходимо согласовывать с точностью, которая требуется для данного размера.

Предельные размеры — два предельно допустимых размера, между которыми должен находиться или которым может быть равен действи¬тельный размер. Больший из двух предельных размеров называют наибольшим предельным размером (Dmax, dmax), а меньший — наименьшим предельным размером (Dmin, dmin) Предельные размеры позво¬ляют оценивать точность обработки деталей.

Отклонение — это алгебраическая разность между действительным и соответствующим номинальными размерами. Отклонения отверстий обозначают буквой E, валов — e.

Действительное отклонение (Er, er) равно алгебраической разности действительного и номинального размеров: Er = Dr — D; er = dr — d.

Предельное отклонение равно алгебраической разности предельного и номинального размеров. Различают верхнее, нижнее и среднее отклонения. Верхнее (ES, es) равно алгебраической разности наибольшего предельного и номинального размеров: ES = Dmax — D; es = dmax — D.

Нижнее отклонение (EI, ei) равно алгебраической разности наименьшего предельного и номинального размеров: EI = Dmin — D; ei = Dmin — D.
Среднее отклонение (Em, em) равно полусумме верхнего и ниж¬него отклонений: Em = 0,5 (ES + EI), em = 0,5 (es + ei).
Пример. Определить предельные и средние отклонения для штифтов, у которых D = 20 мм, dmax = 20,01 мм и dmin = 19,989 мм.

Для графического построения полей допусков и посадок проводят горизонтальную линию 00, называемую нулевой. Нулевая — это линия, положение которой соответствует номинальному размеру и от которой откладываются предельные отклонения размеров. По-ложительные отклонения — вверх от нулевой линии, отрицательные — вниз.

Поле допуска — поле, ограниченное верхним и нижним отклонения¬ми. Оно опре-деляется величиной допуска и его положением относитель¬но номинального размера. При графическом изображении поля допусков показывают зоны, которые ограничены двумя ли-ниями, проведенными на расстояниях, соответствующих верхнему и нижнему отклоне¬нию.
На схемах указывают номинальный D и предельные (Dmax, Dmin, dmax, dmin) размеры, предельные отклонения (ES, EI, es, ei) поля допусков и другие параметры.

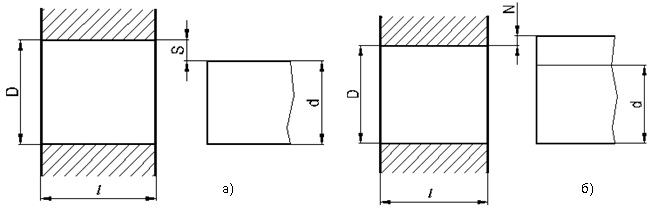
Понятия о посадках и допуске посадки. Если у соединяемых между собой деталей размер отверстия больше размера вала, то в соединении будет зазор (S). Если же размер ва-ла больше размера отверстия, то в соединении будет натяг (N). Зазором называется по-ложительная разность между размерами отверстия и вала S = D — d (рис. 42, а). а натягом — положительная разность между размером вала и отверстия N = d — D (рис. 42, б).

В машинах и приборах требуются посадки с различными зазорами и натягами. В тех случаях, когда одна деталь должна перемещаться относительно другой без качки, следует иметь очень малый зазор: для того чтобы одна деталь могла свободно вращаться в другой (например, вал в отверстии), зазор должен быть больше. Если соединенные вал и втулка представляют собой как бы одно целое, они соединены с натягом и не могут перемещаться относительно друг друга.
Посадки подразделяют на три вида: подвижные, обеспечивающие зазор в соединении: неподвижные (прессовые), обеспечивающие натяг в соединении; переходные, ко-торые наз¬ваны так потому, что до сборки вала и втулки нельзя сказать, что будет в соединении — зазор или натяг, так как заданные отклонения на вал и отверстие перекрывают друг друга.

В зависимости от использованного допуска у той и другой детали при переходной посадке может оказаться, что размер вала больше размера отверстия или размер отверстия больше размера вала.

Для оценки точности соединений (посадок) пользуются понятием допуска посадки, под которым понимается разность между наибольшим и наименьшим зазорами (в посадках с зазором) или наибольшим и наименьшим натягами (в посадках с натягом). В переходных посадках допуск посадки равен разности между наибольшим и наименьшим натягами или сумме наибольшего натяга и наибольшего зазора. Допуск посадки равен также сумме допусков отверстия и вала.

Источник