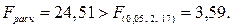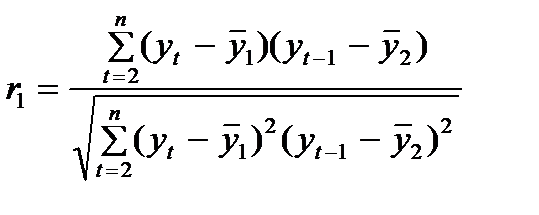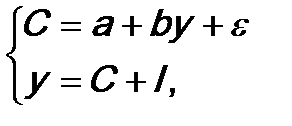Интерпретация параметров модели с фиктивными переменными

Как интерпретируются коэффициенты при фиктивных переменных

Термин “фиктивные переменные” используется как противоположность “значащим” пе­ременным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная пе­ременная, отражающая качественную характеристику. Это могут быть разного рода атрибутивные призна­ки, такие, например, как профессия, пол, образование, климати­ческие условия, принадлежность к определенному региону. Что­бы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. каче­ственные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. В литературе можно встретить термины «структурные переменные» или «искусственные переменные»

Например, в результате опроса группы людей 0 может означать, что опра­шиваемый — мужчина, а 1 — женщина. К фиктивным переменным иногда относят рег­рессор, состоящий из одних единиц (т.е. константу, свободный член), а также временной тренд.

Использование фиктивных переменных в моделях с временными рядами

В регрессионных моделях с временными рядами используется три основных вида фиктивных переменных:

1) Переменные-индикаторы принадлежности наблюдения к определенному периоду — для моделирования скачкообразных структурных сдвигов. Границы периода (моменты “скачков”) должны быть установлены из априорных соображений. Например, 1, если наблюдение принадлежит периоду 1941-45 гг. и 0 в противном случае. Это пример использования для моделирования временного структурного сдвига. Постоянный структурный сдвиг моделируется переменной равной 0 до определенного момента времени и 1 для всех наблюдений после этого момента времени.

2) Сезонные переменные — для моделирования сезонности. Сезонные переменные принимают разные значения в зависимости от того, какому месяцу или кварталу года или какому дню недели соответствует наблюдение.

3) Линейный временной тренд — для моделирования постепенных плавных структурных сдвигов. Эта фиктивная переменная показывает, какой промежуток времени прошел от некоторого “нулевого” момента времени до того момента, к которому относится данное наблюдение (координаты данного наблюдения на временной шкале). Если промежутки времени между последовательными наблюдениями одинаковы, то временной тренд можно составить из номеров наблюдений.

Можно также комбинировать указанные виды фиктивных переменных, создавая переменные “взаимодействия” соответствующих эффектов.

Комбинация рассмотренных фиктивных переменных позволяет моделировать еще один эффект — изменение наклона тренда с определенного момента. Помимо тренда в регрессию следует тогда ввести следующую переменную: в начале выборки до некоторого момента времени она равна 0, а вторая ее часть представляет собой временной тренд (1, 2, 3 и т. д. в случае одинаковых интервалов между наблюдениями).

Использование фиктивных переменных имеет следующие преимущества:

1) Интервалы между наблюдениями не обязательно должны быть одинаковыми. В выборке могут быть пропущенные наблюдения.

2) Коэффициенты при фиктивных переменных легко интерпретировать, они наглядно представляют структуру динамического процесса.

3) Для оценивания модели не приходится выходить за рамки классического метода наименьших квадратов.

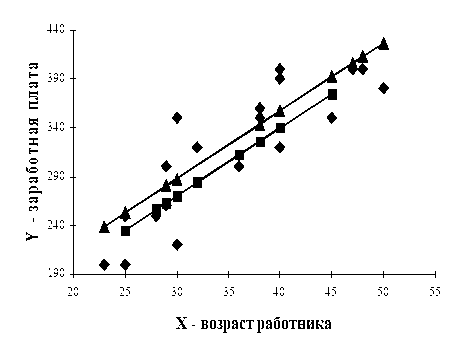
Пример 3.3.6. Требуется построить регрессионную модель зависимости заработной платы работника (Y) от возраста (Х) с использованием фиктивной переменной по фактору пол по 20 работникам одного предприятия (табл. 3.3.17).

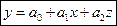
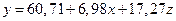
Введем в модель фиктивную переменную Z, которая принимает два значения: 1 – если пол мужской; 0 – если пол женский. Оценим параметры модели методом наименьших квадратов. Для вычислений воспользуемся Пакетом анализа в EXCEL. Уравнение множественной регрессии примет вид:

.

Коэффициент детерминации 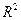равен 0,74.

Уравнение регрессии значимо по F-критерию на 5% уровне, так как

Из полученного уравнения регрессии следует, что при одном и том же возрасте заработная плата у работников мужчин на 17,27$ в месяц выше, чем у женщин.

Из модели, включающей фиктивную переменную можно получить частные уравнения регрессии для работников мужчин (z=1) и женщин (z=0):

Сопоставляя частные уравнения регрессии, видим, что эти уравнения регрессии отличаются значениями свободного члена, а соответствующие линии регрессии параллельны (рис. 3.3.22). График частного уравнения регрессии для мужчин будет располагаться выше, чем график частного уравнения регрессии для женщин.

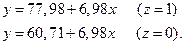
Рис. 3.3.22. Графики частных уравнений регрессии.

Источник

Модели регрессии с фиктивными переменными

До сих в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, таки, например, как профессия, пол, образования, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные должны быть преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называтьфиктивными переменными.

Рассмотрим применение фиктивных переменных для функции спроса. Предположим что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид: где y – количество потребляемого кофе, x – цена.

Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: и женского пола: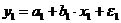

Различия в потреблении кофе проявятся в различии средних и . Вместе с тем сила влияния x на yможет быть одинаковой, т.е. В таком случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной.

где — это фиктивные переменные, принимающие значения:

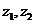
В общем уравнении регрессии зависимая переменная y рассматривается как функция не только цены x, но и пола ( 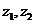). Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. при этом когда , то и, наоборот, при переменная

Для лиц мужского пола, когда и , объединенное уравнение регрессии составит: а для лиц женского пола, когда и Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.

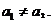
Фиктивные переменные широко используются для оценки сезонных различий в потреблении. Они могут вводиться не только в линейные, но и в нелинейные модели, приводимые путем преобразования к линейному виду.

Прием введения в анализируемую линейную модель регрессии фиктивных переменных используется обычно при работе с неоднородными исходными статистическими данными. Статистическая надежность будет выше. В ходе построения регрессионной модели с фиктивными переменными мы получаем возможность одновременно проверять гипотезы о наличии или отсутствии статистически значимого влияния сопутствующих переменных на структуру анализируемой модели. Однако нельзя рассматривать фиктивные переменные как панацею при применении методов регрессии к неоднородным данным.

69. Понятие временного ряда, его основные компоненты. Задачи изучения временных рядов.

Временной ряд – это последовательность наблюдений некоторой величины в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда (Yt), где t число уровней. Составляющие временного ряда Yt=Ut+Vt+Ct+Et:

· Ut – трэнд, плавно меняющаяся компонента, описывает длительное изменение величины;

· Vt – сезонная компонента, повторяемость экономических процессов в течении не очень долгого периода времени (месяц, год);

· Ct – циклическая компонента, повторяемость экономических процессов в течении длительного периода времени;

· Et – случайная компонента, отражающая влияние не поддающихся учету случайных факторов.

Аддитивные модели представляют собой обобщение множественной регрессии (которая является частным случаем общей линейной модели). Используют операцию сложения (Y=X1+X2+X3).
Мультипликативные модели используют операцию умножения (Y=X1*X2*X3).

1)выявление и количественное определение перечисленных компонент с тем, чтобы использовать полученную модель для прогнозирования будущих значений ряда

2) построение модели взаимосвязи двух или более временных рядов.

70. мультипликативная и аддитивная модели временного ряда

Ввиду четкой интерпретации параметров уравнения наиболее широко используются линейные и степенные функции. Если линейная модель является аддитивной, это означает, что в основе модели лежит гипотеза о том, что каждый фактор что-то добавляет или отнимает от значения результативного признака. Например, если у – это урожайность сельскохозяйственной культуры, а х₁, х₂ и х₃ – агротехнические факторы: дозы удобрений, число прополок, поливов и т.п., то каждый из этих факторов либо повышает, либо понижает величину урожайности, причем последняя могла бы существовать и без этих факторов.

Также часто линейная регрессионная модель используется в функциях потребления (спроса), где у – потребление товара или группы товаров, а факторами могут быть доход семьи в текущем и предшествующем периоде, размер семьи, цены, прошлые привычки потребления, то есть потребление товара в предшествующем периоде.

Параметр а в таком уравнении не подлежит экономической интерпретации, а коэффициенты регрессии рассматриваются как характеристики склонности к потреблению. Например, функция потребления имеет вид

где потребление в период времени t зависит от дохода того же периода D_t и от дохода предшествующего периода D_t-1. Коэффициент в₁ называют краткосрочной предельной склонностью к потреблению. Он показывает, на сколько увеличится потребление товара при увеличении доходов текущего периода на единицу. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на величину b = b₁ + b₂. Коэффициент в рассматривается здесь как долгосрочная склонность к потреблению.

Пример: П (потребление) = 38 + 0,47Д_т +0,23Д_т-1. Краткосрочная склонность к потреблению составляет здесь 0,47, а долгосрочная склонность 0,47+0,23=0,7.

Однако аддитивная модель пригодна не для любых связей в экономике. Если, например, изучается зависимость объема продукции предприятия от занимаемых площадей, числа работников, стоимости основных фондов (или всего капитала), то каждый из факторов является необходимым для существования результата, а не добавлением к нему. В таких ситуациях нужно исходить из гипотезы о мультипликативной форме модели:

(5.1.7)

Такая модель по ее первым создателям получила название модель Кобба-Дугласа. Это степенная функция и, как мы уже знаем, показатели степени при факторах являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 процент при неизменности других факторов. Решение степенной функции методом наименьших квадратов требует предварительной ее линеаризации. Как было рассмотрено ранее (лекция 4), линеаризация степенных функций проводится с помощью логарифмирования ее переменных.

71. Определение сезонной компоненты в мультипликативной и аддитивной моделях

Аддитивной моделью временного ряда называется такая модель, где уровни ряда представлены как сумма трендовой (Т), сезонной или циклической (S) и случайной (Е) компонент: у_t=Т+S+Е. Построению аддитивной модели обычно предшествует анализ структуры временного ряда, то есть определение наличия или отсутствия этих компонент в ряду динамики. Для этих целей строят автокорреляционную функцию. Если коэффициент автокорреляции первого порядка существенно отличен от нуля, то в ряду динамики есть тенденция, если самым высоким оказался коэффициент автокорреляции порядка k, то в ряду есть цикличность в kпериодов времени. Построение аддитивной модели сводится к количественному определению указанных компонент для каждого уровня ряда, определению прогнозных уровней как _t=Т+S и оценке качества модели.

73. Моделирование тенденции временного ряда. Выбор лучшей формы тренда

Один из наиболее распространенных способов моделирования тенденции временного ряда – это подбор и решение математического уравнения, которое бы отражало зависимость уровней ряда от фактора времени. Такие функции называются трендами, а способ построения такой функции – это способ аналитического выравнивания временного ряда.

Зависимость от времени может принимать разные формы, поэтому, как и в случае регрессионных уравнений, для построения трендов могут быть выбраны разные функции:

линейный тренд ;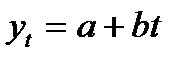

гипербола ;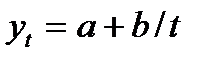

экспонента , где е = 2,71828;

степенная функция ;

парабола и другие.

Параметры таких функций могут быть определены обычным МНК. Параметризация нелинейных трендов требует предварительной их линеаризации.

Как определить форму тренда? Существует несколько способов решения этой проблемы. Самый простой способ – это визуальный анализ графика зависимостей уровней ряда от времени. Второй способ – это определение основных показателей динамики. Если цепные абсолютные приросты для всего ряда примерно равны друг другу, то это линейный тренд; если примерно равны друг другу цепные коэффициенты роста, то функция может быть степенной или показательной. Третий способ определения формы тренда – это анализ коэффициентов автокорреляции. Если временной ряд имеет линейную тенденцию, то его соседние уровни тесно коррелированны, и в этом случае коэффициент автокорреляции первого порядка должен быть очень высокий.

Если есть подозрение на существование нелинейной зависимости, то следует прологарифмировать исходный ряд данных и определить коэффициент автокорреляции первого порядка по логарифмам уровней. Чем сильнее выражена нелинейная тенденция, тем выше будет автокорреляция логарифмов по сравнению с автокорреляцией исходных данных.

Если форму связи всеми перечисленными способами определить достаточно трудно, то перебирают все основные формы трендов, учитывая при этом соотношение числа наблюдений и числа определяемых параметров. Для каждого уравнения определяют коэффициент детерминации и выбирают уравнение с максимальным его значением (экспериментальный способ). Реализация этого метода предполагает компьютерную обработку данных.

Наиболее простую экономическую интерпретацию имеют параметры линейного и показательного трендов. Параметры линейного тренда 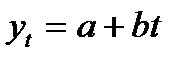интерпретируются следующим образом: Параметр а – начальный уровень временного ряда в момент времени t = 0; b – средний абсолютный прирост уровней ряда за один период.

Если форма тренда описывается параболой, то качественный анализ такого тренда предполагает определение поворотных точек в динамике, замедления или ускорения темпов изменения, начиная с определенного момента времени под влиянием ряда факторов. В случае, если уравнение тренда выбрано неверно, то результаты анализа и прогнозирования динамики временного ряда с использованием выбранного уравнения будут недостоверными вследствие ошибок спецификации.

Для оценки пригодности уравнения тренда для прогноза, также как и для регрессионной модели, может быть рассчитана средняя ошибка аппроксимации

(%) (6.1.3)

Если ее величина не превышает 8-10%, то уравнение тренда может быть использовано в прогнозировании будущих значений результативного признака.

74. Моделирование тенденции при наличии структурных изменений. Критерий Чоу

Метод аналитического сглаживания для выявления тенденции в рядах динамики применим только для качественно однородных периодов. Если в момент (период) времени t* происходили серьезные изменения среды формирования изучаемого показателя (начало крупных экономических реформ, смена политического и экономического курсов, экономические кризисы и т.д.), то необходимо выяснить повлияли ли общие структурные изменения на характер тенденции ряда. И если ряд содержит структурные изменения, то выявлять тенденцию следует по подпериодам: до t* и после t*.

Для оценки возможности построения тренда по данным всего ряда без разбиения на подпериоды используется тест Чоу.

Выдвигается гипотеза о том, что вектор оценок параметров (т.е. оценки всех параметров) тренда по первому подвериоду равен вектору по второму подпериоду, также о равенстве остаточных дисперсий отклонений от линий трендов по этим подпериодам: Н₀: .

, где р – число параметров без свободного члена, — остаточная сумма квадратов при построении тренда по всей совокупности. , — остаточные суммы квадратов для первого и второго подпериодов.

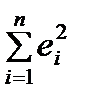
Выбор формы тренда можно осуществить с помощью теста на различие в остаточных дисперсиях:

.

Критическое значение находят при выбранном уровне значимости ( 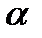) и числе степеней свободы для большей ( ) и меньшей ( ) из двух дисперсий.

В случае выполнения неравенства делается заключение о том, что различия в дисперсиях существенны и функция, которой соответствует меньшая дисперсия, действительно лучше аппроксимирует исходные значения, и именно она выбирается для описания тенденции. Иначе, предпочтение отдается более простой функции.

Необходима оценка существенности уравнения тренда и его параметров в силу того, что сам временной ряд рассматривается как выборка – одна из возможных реализаций случайного процесса.

Средняя ошибка прогноза линейного тренда рассчитывается по формуле: .

75. Автокорреляция уровней временного ряда. Автокорреляционная функция и ее применение при выявлении структуры ряда

Если временной ряд содержит только случайную компоненту, то уровни временного ряда будут независимы друг от друга. Если же временной ряд содержит тенденцию или циклические колебания, то значения каждого последующего уровня зависят от предыдущих.

Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда. Автокорреляцию можно измерить количественно. Для этого рассчитывают линейный коэффициент корреляции между уровнями исходного временного ряда и уровнями этого же ряда, сдвинутыми на один или несколько шагов во времени.

Например, разумно предположить, что доходы домохозяйства в текущем году зависят от доходов домохозяйства предыдущих лет. Определим коэффициент корреляции между ними. Известна рабочая формула линейного коэффициента корреляции

(6.1.1)

В качестве фактора мы рассмотрим доходы предшествующего периода (у_t-1), а в качестве результата – доходы текущего периода (у_t), тогда приведенная выше формула примет вид

где — средний уровень по исходному ряду динамики, определенный без учета первого уровня,

а — это средний уровень по ряду динамики, сдвинутому на одну дату.

Расстояние между уровнями временного ряда, для которых определяется коэффициент корреляции, называется лагом. Приведенная выше формула определяет величину автокорреляции между соседними уровнями, то есть при лаге = 1, поэтому этот коэффициент называют коэффициентом автокорреляции первого порядка. Допустим, r₁ = 0,98. Полученное значение свидетельствует об очень сильной зависимости между доходами текущего и предшествующего периода и, следовательно, о наличии в ряду сильной линейной тенденции.

Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями со сдвигом на две даты, то есть с лагом 2 и т.д.

С увеличением лага число пар, по которым рассчитывается коэффициент автокорреляции, уменьшается и, следовательно, снижается достоверность коэффициентов. Поэтому для обеспечения статистической достоверности лаг не должен быть больше, чем п / 4, где п – число уровней.

При анализе коэффициентов автокорреляции следует помнить следующее:

1) он определяется по формуле линейного коэффициента корреляции, таким образом, он измеряет тесноту только линейной связи текущего и предыдущего уровней временного ряда. Для временных, рядов, имеющих сильную нелинейную тенденцию, коэффициент автокорреляции уровней может быть близким к нулю;

2) Знак коэффициента автокорреляции не указывает на направление тенденции в исходном ряду данных (возрастание или убывание). Большинство временных рядов экономических переменных содержат положительную автокорреляцию уровней, но при этом сам ряд может иметь и отрицательную тенденцию.

Если расположить коэффициенты по величине лага (то есть коэффициенты первого порядка, второго, третьего и т.д.), то мы получим автокорреляционную функцию временного ряда. График зависимости величины коэффициента автокорреляции от лага называют коррелограммой.

76. Моделирование взаимосвязей между признаками на основе рядов динамики. Методы исключения тенденции

Изучение взаимосвязи экономических переменных по данным временных рядов осложнено тем, что в этих рядах может быть тенденция. Если в ряду динамики переменной у и в ряду динамики х есть компонента «Т», то в результате мы получим тесную связь между у и х. Однако из этого факта еще нельзя делать вывод о том, что изменение х есть причина изменения у, то есть что между этими изменениями есть причинно-следственная связь.

Например, за последние 10 – 15 лет в Российской Федерации сократилось поголовье КРС и увеличилось число крестьянских (фермерских) хозяйств. Коэффициент корреляции между уровнями этих рядов динамики высок по величине; знак указывает на обратную связь. Однако это не означает, что рост численности фермерских хозяйств явился фактором снижения поголовья. Чтобы выявить причинно-следственную зависимость между переменными, необходимо устранить ложную корреляцию между ними, вызванную наличием тенденции.

Существует несколько способов исключения тенденции в рядах динамики. Первый способ называется метод отклонений от тренда. Пусть имеется у_t=Т + е и х_t=Т + е. Проводится аналитическое выравнивание каждого ряда: и , где Т_у и Т_х – это оценки трендовых компонент. Затем определяется остаток в каждом наблюдении и

,так как остаточная компонента не содержит тенденции. Далее изучается зависимость между самими остатками е_у=f(е_х). Если между переменными есть связь, то она проявится в согласованном изменении остатков. Недостатком данного способа является то, что содержательная интерпретация параметров такой модели затруднительна. Однако модель может быть использована для прогнозов и, кроме того, коэффициент парной корреляции между остатками отразит связь переменных.

Второй способ преодоления тенденции в рядах динамики – это метод последовательных разностей. Если временной ряд содержит ярко выраженную линейную тенденцию, то для ее устранения можно заменить исходные уровни разностями первого порядка, то есть цепными абсолютными приростами: и . Далее прирост у рассматривается как функция прироста х: . Рассмотрим математическое доказательство исключения тенденции в этом случае.

Мы видим, что величина исключает фактор времени, так как b – константа, а остатки по предпосылкам МНК не должны содержать тенденции, то есть должны быть случайными и независимыми.

Недостатком второго способа является потеря информации (приростов на единицу меньше, чем уровней), что в условиях малого числа наблюдений крайне нежелательно. Достоинством является возможность интерпретации параметров. Коэффициент регрессии b покажет изменение прироста результата при единичном изменении прироста фактора.

Третьим способом является включение в модель регрессии фактора времени: y_t= a+b₁x₁+ b₂ t. В данном случае коэффициенты чистой регрессии легко интерпретируются, имеют естественные единицы измерения. Коэффициент b₁ покажет на сколько единиц изменится результат при единичном изменении фактора при условии существования неизменной тенденции; коэффициент b₂ отразит влияние всех прочих факторов, формирующих тенденцию, кроме x₁. Однако данный способ построения регрессионной модели требует большего объема наблюдений, так как в модели появляется еще один параметр.

Если тренды признаков являются экспонентами (или показательными функциями), то вместо корреляции абсолютных отклонений от трендов можно применить метод корреляции цепных темпов роста уровней, поскольку именно темпы роста – основной параметр экспоненциальных и показательных трендов.

77. Понятие автокорреляции остатков. Статистика Дарбина-Уотсона

При моделировании временных рядов встречаются ситуации, когда остатки содержат тенденцию или цикличность. В этом случае остатки не являются независимыми, каждое последующее значение остатка зависит от предыдущего. Это явление получило название автокорреляция остатков.

Существуют два способа определения автокорреляции в остатках. Первый заключается в визуальном анализе графика зависимостей остатков от времени. Второй способ предполагает использование критерия Дарбина-Уотсона. Величину критерия (d) можно определить по одной из формул

либо d 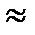2(1 – r_e 1 )

где r_e 1 – коэффициент автокорреляции остатков первого порядка.

Если в остатках существует полная положительная автокорреляция, тоr_e 1 =1 и d = 0. Если в остатках полная отрицательная автокорреляция, то

r_e 1 =-1 и d = 4. Если автокорреляция остатков отсутствует, тоr_e 1 =0 и d = 2.

На практике используется следующий алгоритм проверки гипотезы об автокорреляции остатков:

1. выдвигается нулевая гипотеза об отсутствии автокорреляции в остатках;

2. 2 определяется фактическое значение критерия Дарбина – Уотсона (d);

4. числовой промежуток всех возможных значений d разбивается на 5 отрезков

5. если d- фактическое попадает в зону неопределенности, то предполагают существование автокорреляции в остатках.

В последнем случае исследовать причинно-следственные связи переменных по остаткам нельзя, получим ложную корреляцию.

78. Понятие системы эконометрических уравнений, основные виды

Для описания реальных экономических систем, где статистические показатели находятся во взаимодействии и взаимосвязи, применяются системы эконометрических уравнений. В данных системах случайные переменные называют эндогенными, т.е. внутренними, так как они формируют свои значения внутри модели. Признаки, считающиеся заданными, известными, неслучайными получили название экзогенных, или внешних для данной системы. Один и тот же признак может быть эндогенным в одной задаче и экзогенным – в другой.

Структурная форма модели:

Структурная форма модели содержит при эндогенных переменных коэффициенты , экзогенных переменных – , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня:

Поэтому свободные члены в системе отсутствуют.

Приведенная форма модели:

79. Структурная и приведенная форма модели. Проблема идентификации. Необходимое и достаточное условия идентификации

Для описания реальных экономических систем, где статистические показатели находятся во взаимодействии и взаимосвязи, применяются системы эконометрических уравнений. В данных системах случайные переменные называют эндогенными, т.е. внутренними, так как они формируют свои значения внутри модели. Признаки, считающиеся заданными, известными, неслучайными получили название экзогенных, или внешних для данной системы. Один и тот же признак может быть эндогенным в одной задаче и экзогенным – в другой.

Структурная форма модели:

Структурная форма модели содержит при эндогенных переменных коэффициенты , экзогенных переменных – , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня:

Поэтому свободные члены в системе отсутствуют.

Приведенная форма модели:

При переходе от приведенной к структурной форме возникает проблема идентификации, то есть однозначности определения параметров структурной модели от приведенной формы. Переход необходим, поскольку экономический смысл и интерпретацию имеют только параметры структурной формы.

Условия идентифицируемости проверяются для каждого уравнения в отдельности.

Счетное (необходимое) условие идентифицируемости:

Чтобы уравнение было идентифицируемым, нужно, чтобы:

где n_x – число экзогенных переменных, содержащихся в системе, но отсутствующих в данном уравнении системы;

n_y – число эндогенных переменных в данном уравнении.

Если 1+n_x n_y, то уравнение сверхидентифицируемо.

Ранговое условие идентифицируемости (достаточное):

Для разрешимости системы структурных уравнений достаточно, чтобы ранг матрицы, составленной из коэффициентов эндогенных и экзогенных переменных, отсутствующих в данном уравнении, но присутствующих в других уравнениях системы, был не меньше, чем число эндогенных переменных в системе без одного, а определитель этой же матрицы не был равен нулю.

80. Косвенный метод наименьших квадратов

В системе рекурсивных уравнений хоты бы одна эндогенная переменная должна определятся только лишь набором независимых переменных. Если все эндогенные переменные расположены в левой части, а экзогенные – в левой, то такая система называется системой независимых уравнений. Для решения систем независимых и рекурсивных переменных используется метод наименьших квадратов.

Препятствие к применению метода наименьших квадратов, которое заключается в коррелированности эндогенных переменных со случайными членами легко преодолеть, если:

1) привести систему к виду, чтобы в правой части оставались только экзогенные переменные. Такая форма называется приведенной;

2) затем применить метод наименьших квадратов к каждому уравнению в приведенной форме и получить оценки ее параметров;

3) перейти от приведенной формы к структурной, проведя процедуру обратного преобразования параметров.

Эта методика получила название косвенного метода наименьших квадратов и позволяет получать состоятельные и несмещенные оценки параметров структурной форму системы одновременных уравнений.

Двухшаговый МНК является универсальным, позволяет решать как точно идентифицируемые, так и сверхидентифицируемые системы структурных уравнений. Значимость этого метода определяется тем, что он позволяет решать сверхидентифицируемые системы, оценить которые косвенным методом нельзя.

Сверхидентифицируемые системы бывают двух типов:

· все уравнения системы сверхидентифицируемы;

· система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Для второго типа в отношении идентифицируемых уравнений может применяться косвенный МНК, для сверхидентифицируемых уравнений и систем, где все уравнения сверхидентифицируемы, следует применять двухшаговый МНК.

Двухшаговый МНК реализуется в следующей последовательности:

1) сначала нужно привести систему к приведенной форме;

2) затем применить МНК к каждому уравнению в приведенной форме и получить оценки ее параметров;

3) находят расчетные значения эндогенных переменных, подставляя значения экзогенных переменных в соответствующие приведенные уравнения по всем единицам совокупности.

4) подставляют в структурную форму фактические значения экзогенных переменных и тех эндогенных переменных, которые находятся в левой части, и расчетные значения эндогенных переменных, находящихся в правой части системы, а затем применяют метод наименьших квадратов. Замена фактических значений эндогенных переменных, находящихся в правой части системы, решает проблему их коррелированности с ошибками регрессии.

Двухшаговый метод наименьших квадратов дает такие же оценки, как и косвенный метод.

Для оценки надежности параметров структурной формы может применяться дисперсионный анализ.

Проверку значимости целесообразно проводить еще на стадии получения системы приведенных уравнений. Продолжать реализацию косвенного и двухшагового методов следует лишь в случае получения значимых приведенных уравнений.

82. Модель Кейнса. Инвестиционные мультипликаторы потребления и национального дохода.

Наиболее широко системы одновременных уравнений применяются для моделирования макроэкономики. Большинство из них построено на основе кейнсианских моделей. Статическая модель Кейнса для описания народного хозяйства страны в наиболее простом варианте имеет следующий вид (в современных показателях системы национального счетоводства России):

где С – конечное потребление в постоянных ценах;

у – валовой располагаемый национальный доход (ВРНД) в постоянных ценах;

– случайная составляющая;

I – валовые инвестиции в постоянных ценах (валовое сбережение).

Второе уравнение является тождеством, поэтому структурный коэффициент bне может быть больше 1. Он характеризует предельную склонность к потреблению.

Система приведенных уравнений:

Приведенная форма модели содержит мультипликаторы:

— инвестиционный мультипликатор потребления:

;

— инвестиционный мультипликатор национального дохода:

.

Мультипликаторы интерпретируются как коэффициенты линейной регрессии, т.е. они показывают, на сколько единиц изменится эндогенная переменная, если экзогенная переменная изменится на единицу.

Источник